
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретичні відомості. Розглянемо приклад моделювання процесу зміни температури в стінці, що описується диференційними рівняннями в частинних похідних
|
|
Розглянемо приклад моделювання процесу зміни температури в стінці, що описується диференційними рівняннями в частинних похідних. Однорідна стінка товщиною L великої площі поділяє два середовища з різною температурою: на лівій поверхні температура змінюється за часом, як функція j 1(t), на правій – якфункція j 2(t).
Потрібно відтворити процес зміни температури для внутрішніх точок стінки. Для цього проведемо вісь y перпендикулярно стінці. Температура внутрішніх точок стінки – функція двох змінних: часу t і координати y, тобто v (t, y). Точки стінки, що знаходяться на одній вертикалі, мають однакову температуру внаслідок великої площі стінки і її однорідності. Функція v (t, y) задовольняє наступному рівнянню:
 , (2.1)
, (2.1)
де l – коефіцієнт теплопровідності стінки, с – питома об'ємна теплоємність стінки.
Рішення рівняння повинне відповідати крайовим умовам v (t, 0) = j 1(t), v (t, L) = j 2(t) і початковій умові v (0, y) = T (y).
Для отримання системи звичайних диференціальних рівнянь, що апроксимують рівняння теплопровідності, розіб'ємо стінку вертикальними лініями на ряд шарів однакової товщини. При перетині цих прямих з віссю y утвориться ряд точок. Для кожної з цих точок температура буде функцією однієї змінної – часу. Будемо вважати, що точки на осі y розташовані одна від одної на невеликій однаковій відстані h. Підставимо координати yi точок i у рівняння теплопровідності:
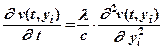 . (2.2)
. (2.2)
Позначимо v (t, yi) через vi (t), то  .
.
Частинну похідну 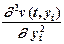 приблизно можна знайти через значення функції v (t, y) у точці yi та двох сусідніх з нею точках i +1 і i – 1:
приблизно можна знайти через значення функції v (t, y) у точці yi та двох сусідніх з нею точках i +1 і i – 1:
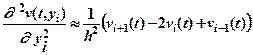 , (2.3)
, (2.3)
де vi+ 1(t) = v (t, yi+ 1), vi– 1(t) = v (t, yi– 1).
З урахуванням цих виразів отримаємо звичайні диференційні рівняння першого порядку:
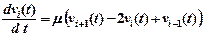 ,
,
де vi (0) = T (yi) = Ti, m =(l / c)/ h 2.
Таких рівнянь буде стільки, скільки точок було виділено на осі. Якщо точок n, то всі рівняння разом складуть систему з n диференційних рівнянь. Наприклад, для чотирьох точок при vi (0) = Ti , v (t, 0) = j 1(t), v (t, L) = j 2(t) система рівнянь буде наступна:
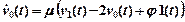 ,
,
 ,
,
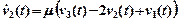 ,
,
 .
.
Таку систему рівнянь можна розв’язати за допомогою будь-яких методів чисельного інтегрування (наприклад, методом Рунге-Кутта).