
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Порядок виконання завдання
|
|
1. Промоделюйте лінійну коливальну систему, використовуючи метод інтегрування Рунге-Кутта четвертого порядку.
Система описується рівнянням:
 ,
,
де a 1 = 0.5; a 2= 39.4784176.
Нехай  .
.
Тоді отримаємо наступну систему рівнянь:
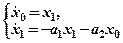
Для моделювання такої системи в середовищі пакету Mathcad задайте вектор початкових умов y, вектор правих частин D(t, x) та для чисельного інтегрування використовуйте вбудовану функцію Z: = rkfixed(x, Tn, Tk, N, D), де x – вектор початкових умов; Tn=0, Tk – початковий та кінцевий часи моделювання; N – кількість точок інтегрування(N=(Tk-Tn) / hінт); D – вектор правих частин.
Початкові умови та кінцевий час моделювання необхідно обрати з таблиці 1.1 згідно варіанту.
Крок інтегрування hінт можна прийняти рівним від 0.01 до 0.1.
Таблиця 1.1
| № | |||||||||||
| y (0) | -4 | -10 | -5 | -8 | |||||||
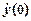
| 0.4 | 1.0 | -1.2 | 0.2 | 0.7 | 1.5 | 0.8 | -0.6 | 1.2. | 0.5 | |
| Tk, c | |||||||||||
2. Промоделюйте систему, що описується диференційним рівнянням четвертого порядку з заданими початковими умовами та вхідному впливі:
 де
де  .
.
Параметри а 1, а 2, а 3, а 4, А, w, j, k, початкові умови y (0), 
 ,
,  та кінцевий час моделювання Tk оберіть з таблиці 1.2.
та кінцевий час моделювання Tk оберіть з таблиці 1.2.
Для цього перетворіть задане диференційне рівняння четвертого порядку до системи з чотирьох рівнянь першого порядку, виконавши наступну заміну змінних:

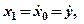


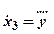 .
.
3. Перевірте властивість адитивності лінійної системи, спостерігаючи, як змінюються в часі змінна (х 0) та її похідна (х 1):
- промоделюйте систему з нульовими початковими умовами та вхідному впливі f (t );
- промоделюйте систему з заданими початковими умовами та без вхідного впливу f (t );
- проведіть графічне порівняння суми отриманих рішень з рішенням за п.2.;
4. Перевірте властивість однорідності лінійної системи, спостерігаючи, як змінюються в часі змінна (х 0) та її похідна (х 1):
- промоделюйте систему з заданими початковими умовами, помноженими на коефіцієнт k та вхідному впливі f (t ), помноженому на коефіцієнт k;
- проведіть графічне порівняння отриманих рішень з рішеннями за п.2, які помножені на коефіцієнт k.
Таблиця 1.2
| № | ||||||||||
| а 1 | 0.5 | 0.2 | 0.25 | 0.75 | 0.6 | 0.3 | 0.06 | 0.5 | 0.4 | 0.2 |
| а 2 | 0.16 | 0.15 | 1.2 | 0.8 | 0.6 | 0.4 | ||||
| а 3 | 0.01 | 0.01 | 0.025 | 0.08 | 0.1 | 0.8 | 0.012 | 0.02 | ||
| а 4 | 0.002 | 0.04 | 0.002 | 0.04 | 0.12 | 0.005 | 0.015 | |||
| А | 0.6 | 0.2 | 1.5 | |||||||
| w | p/ 2 | p/ 4 | p/ 4 | p/ 3 | p/ 4 | p/ 2 | p/ 2 | p/ 3 | p/ 6 | p/ 4 |
| j | p/ 12 | p/ 6 | p/ 8 | p/ 12 | p/ 8 | p/ 4 | -p/ 8 | p/ 6 | p/ 12 | p/ 10 |
| y (0) | –40 | –5 | –20 | –10 | 1.5 | 2.5 | –4.5 | |||

| –0.5 | –2 | –5 | 2.5 | 1.5 | |||||

| –8 | –10 | –5 | –2 | –1. | –0.8 | –0.2 | |||

| ||||||||||
| k | ||||||||||
| Tkін |