
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретичні відомості. Для рішення ЗДР n-го порядку чисельними методами його необхідно призвести до системи, що складається з n диференційних рівнянь першого порядку
|
|
Для рішення ЗДР n -го порядку чисельними методами його необхідно призвести до системи, що складається з n диференційних рівнянь першого порядку. Методику такого приведення розглянемо на прикладі ЗДР другого порядку:
 (1)
(1)
при початкових умовах 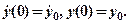
Введемо нові змінні
 (2)
(2)
та розв'яжемо рівняння (2.1) щодо старшої похідної:
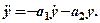 (3)
(3)
Зробивши підстановку нових змінних (2) в (3), одержимо систему з двох ЗДР першого порядку:
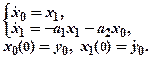 (4)
(4)
Зверніть увагу, у правих частинах рівнянь відсутні похідні змінних і система не містить початкової змінної y та її похідних.
Систему рівнянь (2.4) можна записати у векторній формі:
 (5)
(5)
де 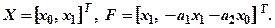
Для дослідження багатьох технічних і природних систем їх можна представити шляхом лінеаризації і допущень як лінійні системи. При цьому рівняння мають лінійний вигляд, тобто в них відсутні нелінійні функції від змінних, а методи дослідження простіші.
Лінійні системи мають властивості однорідності й адитивності. Якщо система лінійна, то вона описується векторним рівнянням:
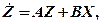 (6)
(6)
де Z – вектор стану системи, X – вектор зовнішніх впливів на систему, A и B – матриці відповідних розмірів.
Властивість адитивності виражається таким співвідношенням:
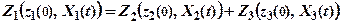 , (7)
, (7)
де 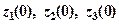 – початкові стани систем,
– початкові стани систем,
причому 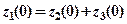 ,
,
 – зовнішні впливи на системи,
– зовнішні впливи на системи,
причому 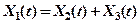 .
.
Властивість однорідності задовольняє таке співвідношення:
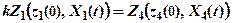 , (8)
, (8)
або 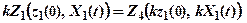
де  – початкові стани систем, причому
– початкові стани систем, причому 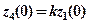 ,
,  – зовнішні впливи на системи, причому
– зовнішні впливи на системи, причому  ,
,
k – коефіцієнт пропорційності.
З приведених співвідношень (7) та (8) очевидна властивість декомпозиції:
 ,
,
яке можна використовувати для дослідження лінійності систем.
Таким чином, лінійну систему можна досліджувати частинами. Наприклад, досліджувати її при нульових початкових умовах, з тестовими впливами, потім при нульових вхідних впливах із різними початковими умовами. Або одержати рішення при одиничних вхідних впливах, а будь-які інші рішення отримати шляхом множення його на відповідний коефіцієнт k.