Дослідження екологічної системи

Однією з найпростіших моделей екологічних систем є модель, що описує боротьбу двох видів – хижака і жертви.

Розглянемо певний замкнутий простір, у якому живуть два види істот. Наприклад, це може бути ліс, у якому живуть вовки і зайці, або ставок, у якому живуть карасі і щуки.

Позначимо через x – кількість жертв (зайців, карасів), а y – кількість хижаків (вовків, щук). Припустимо, що, якщо вовків у лісі немає, тоді зайці розмножуються за експоненціальним законом (1.4). З іншого боку, при відсутності жертв хижаки вимирають за експоненціальним законом (1.5). Цей процес описується наступними диференційними рівняннями:

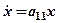, (1.4)

. (1.5)

Припустимо, що кількість зустрічей хижаків із жертвами пропорційна їхньому добутку. Зрозуміло, кількість жертв буде зменшуватися при зустрічі з хижаками, а кількість хижаків буде збільшуватися, і диференційні рівняння (1.4, 1.5) з урахуванням числа зустрічей будуть мати вигляд:

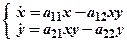. (1.6)

Наведені рівняння називаються рівняннями Лотка-Вольтерра.