Порядок виконання роботи. 1. Промоделюйте екологічну систему, використовуючи метод інтегрування Рунге-Кутта четвертого порядку

1. Промоделюйте екологічну систему, використовуючи метод інтегрування Рунге-Кутта четвертого порядку. Для моделювання такої системи зробіть наступні заміни.

Нехай х ₀ = x, х ₁ = y.

Тоді отримаємо наступну систему рівнянь:

.

Параметри та початкові умови системи задайте наступними:

a ₁₁ = 0.06, a ₁₂ = 0.0006, a ₂₁ = 0.0006, a ₂₂ = 0.24, x (0)= 500, y (0)= 300. Час спостереження за системою 150 днів. Крок інтегрування прийняти рівним hіnt =0.1 дня.

Для моделювання такої системи в середовищі пакету Mathcad задайте вектор початкових умов х, вектор правих частин D(t, х) та для чисельного інтегрування використовуйте вбудовану функцію Z: = rkfixed(х, 0, Tk, N, D), де х – вектор початкових умов, Tн, Tk – початковий та кінцевий часи моделювання, N – кількість точок інтегрування (N: =Tk/ hіnt), D – вектор правих частин.

2. Побудуйте графіки зміни у часі кількості хижаків та жертв. В середовищі пакету Mathcad для цього будуються графіки залежнос­тей , , 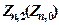де – вектор часу, – вектор першої змінної, – вектор другої змінної, n змінюється від 0 до N-1.

3. Побудуйте графік залежності хижаків від жертв 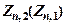. Визначить точку стаціонарного стану системи (yst, xst), у якому приріст жертв урівноважений діяльністю хижаків, а приріст хижаків – їхньою природною смертністю.

4. Промоделюйте систему за умови відсутності зустрічей хижаків із жертвами.

5. Промоделюйте процес поширення епідемії, використовуючи метод інтегрування Рунге-Кутта четвертого порядку. Для моделю­вання такої системи зробіть наступні заміни: х ₀ = x, х ₁ = y, х ₂ = z.

Тоді отримаємо наступну систему рівнянь:

,

Розробіть програму моделювання процесу поширення епідемії в середовищі пакету Mathcad, використовуючи вбудовану функцію rkfixed().

Параметри та початкові умови системи задайте наступними:

Н = 1000, b = 1, g = 10, x (0) = 900, y (0) = 90, z (0= H – x (0)– y (0).

Час моделювання – 40 днів. Крок інтегрування – 0.1 день.

6. Побудуйте графіки зміни у часі кількості здорових, хворих та перехворілих людей.

7. Промоделюйте систему при умові, що у визначений день вдалося ізолювати захворілих людей від здорової частини населення. Відобразіть процес на графіку.

1.5 Контрольні запитання

1. Що таке моделювання? Для чого воно призначено?

2. Приведіть деякі типи моделей.

3. Дайте визначення поняттям система та її чотирьом ознакам.

4. Які методи інтегрування Ви знаєте? Чим вони відрізняються?

5. Які допущення в описах систем дозволяли виділити їх із навколишнього середовища?