Ограниченность и норма линейного оператора.

Пусть А: х-> у х, у – Банахово пространство, А х0 принадлежит Х, если из того, что

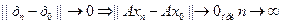где 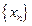- произвольная последовательность из окресности х0

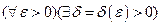из

Если А непр. в каждом эл-те нек.мн-ва, то он непр-н на этом мн-ве, в частности, если х0-произвольный эл-т, для любого х0из х

Лиин.оператор непрерывен на всем пр-ве тогда и только тогда, когда он непр-н в нулевом эл-те. Оператор А наз-ся огранич-м, если для любого х из Х, выполн-ся: 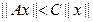С-const 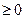(1)

Теорема.

Лиин.оператор А: х-> у непр-н тогда и только тогда, когда он ограничен.

Рассмотрим неравенство, кот. Выполняется для лин-го ограниченного оператора, для конкретного оператора А в неравенстве (1), const С может быть больше с сохранением этого неравенства, однако, уменьшение константы не всегда возможно.

Х не равно пустому множеству, рассмотрим эквивалентное нерав-во 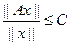(2) min возможен с совпадением с max, возможен sup значение левой части неравенства

Число норма А определяется равенством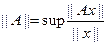

Называется нормой лин.ограниченого оператора А.Из (3) следует

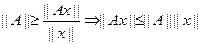
В отличие от (1) в этом неравенстве величина А= 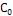яв-ся наименьшей возможно константой.