Полные и неполные нормированные пространства.

Пусть Х- нормированное пространство с нормой ||. || счётное, упорядоченное мн-во элементов {Xn}от 1 и до ∞, или {Xn}будем называть последовательностью если выбраны некоторые члены последовательности {Xnk}то получим последовательность, называющуюся подпоследовательностью.

Понятие нормы(а значит и метрики)позволяет определить сходимость последовательности, как известно из анализа, если численная последовательность удовлетворяет условию Коши, то она сходится(критерии сходимости), однако в ФАНе эти понятия разделяются.

Опр 4.1 Последовательность {хn}Є х сходящаяся к элементу хo Є Х (хn→ хo при n→ ∞), если || хn- хo ||→ 0 при n→ ∞ bn = || хn- хo ||.

Данное определение принимается за основное и допускает эквивалентную переформулировку:

При любом ε > 0 сущ-ет N=N(ε) такой что u > = N для всех элементов || хn- хo || < ε для сход-ся послед-ей норм. пр-ва сост.основным аналогом о сходимости:

1)если последовательность сх-ся то предельный элемент один.

2)если последовательность сх-ся то любая её последовательность сх-ся к этому же элементу.

3)над сх-ся последовательностью можно производить элементарные алгебр.действия.

(хn→ хo и уn → уo ≥ хn± уn; λ n→ λ и хn→ хo, то λ n* хn→ λ o* хo)

Опр 4.2 Посл-сть {хn} фундаментальная если для любого произв.фикс. р || хn+р- хo ||→ 0.

Р! След. нерав-во || хn+р- хo || = || (хn+р- хo)+(хo - хn)||≤ || хn+р- хo ||+|| хn- хo ||.

Из сходимости следует фундаментальность, обратное- не верно.

Опр 4.3 Пусть пространство Х такое, что в нём любая фунд. посл-ть сх-ся к элементу данного пространства, тогда пр-во полное или Банаховое.

Банохово пр-во обладает рядом свойств классического нормированного пространства. Для известных норм. пр-в, норма определяет определённый вид сходимости, который можно охарактеризовать в терминах данного пространства.

Rn-линейное пр-во x=(x1, x2…xn) относительно любых из след. норм:

1) || х ||1=| x1|+ | x2|+…+| xn|=Σ (от i=1 до n) |xi|.

2) || х ||2=(Σ (от i=1 до n) |xi| 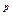) 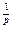, 1< p< ∞

3) || х ||3=max{| x1|+ | x2|+…+| xn|}=max|xi|

Примеры неполного норм.пр-ва.

Для построения примера неполного пр-ва достаточно на полн. пр-ве определить норму и в полученой норм. пр-ве доказать существование хотя бы 1 послед-ти, которая явл. фундаментальной по этой норме не сх-ся к элементам этого пространства, в качестве лин-го пр-ва фун-ии и для определённостей.

Пространство С[-1; 1] с нормой || х ||= 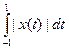является не полным нормированным пространством.