Компактные множества.

12.1. В математическом анализе известен принцип Больцано - Вейерштрасса о возможности выделения из любой ограниченной числовой последовательности сходящейся подпоследовательности: Если на числовой оси задано множество А, то для того, чтобы из любой последовательности можно было выделить частичную, сходящуюся к конечному пределу, необходимо и достаточно, чтобы множество А было ограничено.

При переходе в произвольное метрическое пространство мы уже не получим такого простого результата. Однако, существуют множества, называемые компактными, где такое выделение возможно.

Пусть Х - произвольное метрическое пространство. Множество 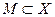называется компактным, если из любой последовательности 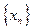элементов этого множества можно выделить сходящуюся подпоследовательность.

Если пределы таких подпоследовательностей принадлежат М, то множество М называется компактным в себе. Ясно, что множество компактно в себе, если оно просто компактно и замкнуто.

Может оказаться, что всё метрическое пространство Х компактное (очевидно, в себе) множество. В этом случае Х называют компактом.

Примеры:

1. Множество точек отрезка 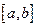компактно в силу теоремы

Больцано - Вейерштрасса.

2. Множество точек всей прямой не компактно, т. к. последователь-ность { 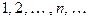} не содержит никакой сходящейся подпоследовательности.

Следует отметить, что свойством компактности наряду с отрезками обладают все замкнутые ограниченные множества эвклидова пространства любой конечной рвзмерности.

- 34 -

Напротив, плоскость, прямая, трехмерное пространство служат простейшими примерами некомпактных пространств.

12.2. ТЕОРЕМА 1. Каждое компактное пространство полно.

Доказательство:

Пусть 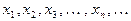- фундаментальная последовательность элементов компакта, т. е. можно указать номер 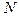такой, что для всех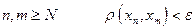

Так как мы рассматриваем компакт, то наша фундаментальная последовательность содержит сходящуюся подпоследовательность. Пусть 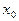- предельная точка этой подпоследовательности. Покажем, что 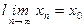. Для доказательства достаточно выбрать число 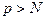такое, что . Это возможно, если выбрать 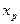из той подпоследовательности, которая сходится к .

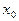Тогда по неравенству треугольника:

, т. к. .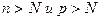

Ч. Т. Д.

12.3. Некоторым расширением компактного пространства является предкомпактное пространство.

Метрическое пространство М называется предкомпактным, если всякая бесконечная последовательность точек из М содержит фундаментальную подпоследовательность.

12.4. Пусть 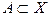некоторое множество метрического

пространства Х и 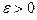- заданное число. Множество 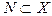называется 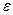- сетью множества А, если для любого 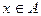существует такая точка 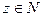, что .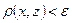

ТЕОРЕМА 2. Всякое компактное множество при

любом 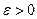имеет содержащуюся в нем самом конечную 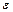- сеть (т. е. 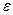- сеть, состоящую из конечного числа точек).

Доказательство:

Пусть М - компактно, но допустим, что при некотором 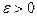конечной 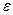- сети не существует во множестве М.

Возьмем любую точку 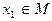. Очевидно, существует такая точка 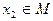, для которой 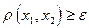. В противном случае уже одна точка 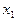образовывала бы 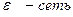в М.

Пусть уже определены точки 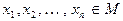такие, что 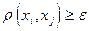при 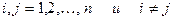. Так как по предположению конечное множество точек 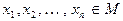не может составлять 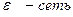для множества М, то существует такая точка 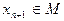, что

, ,..., .

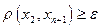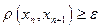Продолжая этот процесс, мы строим такую бесконечную последовательность точек 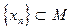, для которой 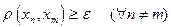. Но из такой последовательности нельзя выделить никакой сходящейся подпоследовательности, а это противоречит компактности М. Таким образом, при 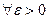в М существует конечная 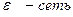. Ч. Т. Д.

8. Критерий компактности в С[ a, b ].