
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метрические пространства.
|
|
Метри́ ческим простра́ нством называется множество, в котором определено расстояние между любой парой элементов.
На одном и том же множестве могут быть заданы различные функции расстояния, или, что тоже самое, метрики: каждая метрика задаёт своё метрическое пространство.
Каждое нормированное или евклидовое пространство является в то же время и метрическим пространством, поскольку заданные в них норма и скалярное произведение порождают соответствующую им функции расстояния.
Всякое метрическое пространство является вместе с тем и топологическим пространством, в частности, метрическое пространство является хаусдорфовым пространством — топологическим пространством, в котором любые две различные точки отделимы друг от друга. Важнейшая часть исследований в общей топологии посвящена решению вопроса о метризуемости тех или иных топологических пространств.
Особое место среди метрических пространств занимают полные метрические пространства, в которых сходится каждая фундаментальная последовательность.
Метрическое пространство есть упорядоченная пара 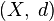 , где
, где 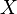 — множество элементов (точек) произвольной природы, а
— множество элементов (точек) произвольной природы, а 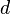 — числовая функция, которая определена на декартовом произведении
— числовая функция, которая определена на декартовом произведении 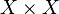 , принимает значения в множестве вещественных чисел и удовлетворяет трём аксиомам — аксиомам метрического пространства — и, в соответствии с этим называется функцией расстояния или метрикой. Каждая метрика порождает на одном и том же множестве своё метрическое пространство: вообще говоря,
, принимает значения в множестве вещественных чисел и удовлетворяет трём аксиомам — аксиомам метрического пространства — и, в соответствии с этим называется функцией расстояния или метрикой. Каждая метрика порождает на одном и том же множестве своё метрическое пространство: вообще говоря, 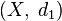 и
и 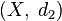 — различные метрические пространства для
— различные метрические пространства для 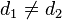 .
.