Обратимость суммы операторов.

Пусть Х – банахаво пр-во

В: Х 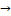Х лин. огран. Оператор

Рассмотрим условия(достаточные) обратимости (I + В): Х 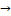Х, где I: Х 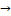Х единичный оператор.

Многие задачи приводятся к вспомогательному операторному ур-ию вида

х + Вх = у или (I + В) х = у.

Пример задача Коши .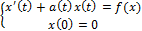

Рассмотрим вспомогательные понятия

Для оператора В: Х 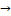Х определяет натур. Степени n=1, 2… следующим образом

….

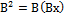
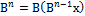
Далее положим, 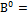I

Рассмотрим формальный оператор Rx, R: Х 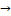Х опр-ый равенством

Rx = х - Вх + 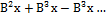- сумма бесконечна

Может быть записан в виде 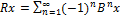(1)

Ряд (1) построенный для оператора В наз. Рядом Неймана. Этот формальный ряд(т.к. сумма в правой части имеет смысл если ряд сходится в банаховом пространстве) даст представления алгебраического обратного оператора для I + В при условии его существования.

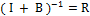
Для проверки этого утверждения надо убедиться в справедливости 2-ух равенств

1)

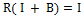
2)

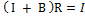
Убедимся в справедливости первого равенства (второе проверяется так же). Для удобства оператор R (ряд неймана) представляем в виде

…

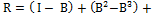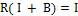
Т. О. Если предположить, что алгебраический обратный для 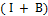существует, то он представляется в виде ряда Неймана.

Т.О. доказано, что при условии существования алгебр. Обратимости для оператора

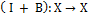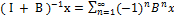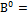является оператор предст. В виде ряда неймана т.е. , где I

Кроме этого нам потребуется следующая оценка произвольной степени оеператора В. Имеем:

………..

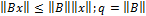
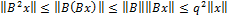
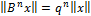
то устанавливает оценку

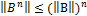
Теорема. Пусть В: Х 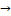Х – лин огр оператор и , тогда (I + В) обратим при этом справедливо неравенство

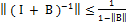
Док-во. Будем предпологать что алгебр. Обр. существует (т.е. это непосредственно проверяеться с приминением опер-ем алгебр. Обр. оператора, остается док-ать, что алгебр. Обр. оператор явл. Ограниченым. Докажем это с применением представления алгебр. Обр. в виде ряда неймана) имеем: 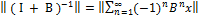оценим выражение в правой части, ксли бы ∑ содержала конечное число слагаемых то по неравенству треугольнильника можно оценить суммой норм; в данном случае можно оценить n-ую частичную ∑ затем перейти к пределу

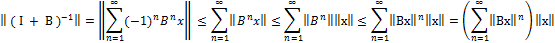
Сумма в скобках явл. Суммой бесконечно геом. Прогрессии со знаменателем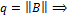

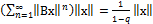
Если сравнить левую часть с полученным выражением, то получим