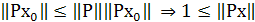Проекторы.

Линейный оператор Р называют проектор тогда, и только тогда, когда 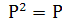(повторное использование не меняет значение)

В качестве определения можно использовать следующее свойство проектора: линейный оператор 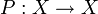является проектором, если и только если существуют такие подпространства 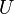и 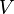пространства 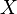, что 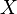раскладывается в их прямую сумму, и при этом для любого элемента 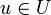имеем 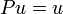, а для любого элемента 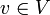имеем 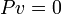. Подпространство 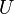называется образом, а 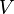— ядром проектора .

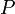Свойства проекторов:

· Пусть 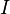— тождественный оператор. Если 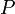- проектор, то 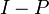- тоже проектор, причём 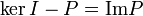и .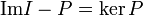

· В конечномерном нормированном пространстве все проекционные операторы непрерывны.

· Для банахова же пространства проекционный оператор будет непрерывным, если его образ замкнут, при этом ядро проектора тоже окажется замкнутым. Таким образом, непрерывный проектор задаёт разложение пространства в прямую сумму замкнутых подпространств: .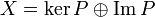

· Собственными значениями проектора могут быть только 0 и 1. Соответствующими собственными подпространствами проектора будут его ядро и образ.

T1. Для нетривиального лин.огр. проектора Р: Х 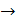Х справедливо неравенство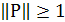

Док-во: имеем