Открытые множества и замкнутые множества.

ОТКРЫТЫЕ МНОЖЕСТВА.

Назовем открытым 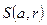(замкнутым 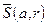) шаром с центром в точке а и радиусом r множество элементов х метрического пространства Х, удовлетворяющих, соответственно, условиям:

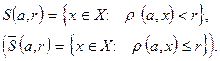
Примеры: 1. В 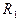(на числовой оси):

2. В С(a, b): 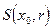составляют множество непрерывных функций, графики которых не выходят из полосы шириной :

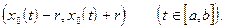
7.2. Окрестностью точки х называют любой открытый

шар с центром в этой точке.

Точка 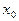называется внутренней, если она входит во множество вместе со своей окрестностью.

Множество 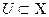- открытое, если все его точки внутренние.

Пример: (a, b) - открытое множество.

7.3. ТЕРЕМА 1. Открытый шар с центром в некоторой

точке 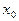и радиусом 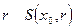- открытое множество.

Доказательство:

Пусть .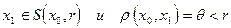

Построим .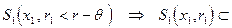

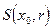Действительно: для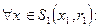

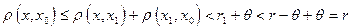
Ч.Т.Д.

ТЕОРЕМА 2. Объединение открытых множеств в любой совокупности и пересечение открытых множеств в конечном числе есть открытое множество, т.е.:

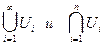- открытые множества.

Доказательство:

1. 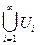открытое множество из определения. Действительно, если

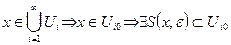, т.к. U - открытое множество. Но

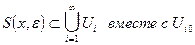. Ч.Т.Д.

2. 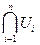- открытое множество. Действительно, для 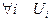-открытое

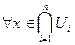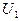
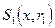множество, тогда входит в с шаром , в 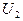с шаром 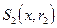,..., в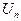 с шаром 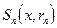. Следовательно,

. Ч.Т.Д.

Для 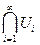утверждение неверно, т.к. 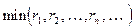бесконечного множества положительных чисел может быть равен нулю.

Пример: 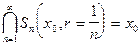- не открытое множество.

Замкнутые множества. Замыкание.

.Множество 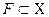называется замкнутым, если оно содержит в себе все свои предельные точки.

Примеры: 1. Множество точек отрезка 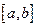образуют замкнутое множество. Из математического анализа известно, что все точки отрезка являются предельными, вне отрезка нет точек предельных для точек множества.

2. Множество точек интервала 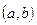образуют незамкнутое множество.

Действительно, точки a и b предельные для точек данного множества, но множеству не принадлежат.

3. Множество всех действительных чисел 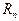(точек числовой оси) - замкнутое множество.

Замыканием множества М называется множество 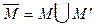, где 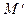- производное множество (множество предельных точек М).

Очевидно, М - замкнутое множество, если . Напротив, если М - замкнутое множество, то 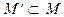и, следова-

тельно, 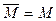(Это утверждение можно считать вторым определением замкнутого множества: множество замкнуто, если оно совпадает со своим замыканием).

Примеры: 1. Для мн-ва .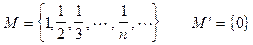

Тогда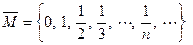

2. Для - пустого множества имеем: .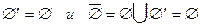

Следовательно, - замкнутое множество.

ТЕОРЕМА 1. В любом метрическом пространстве замкнутый шар 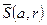есть замкнутое множество.

Доказательство:

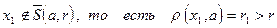Пусть . (1)

Докажем, что 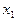не предельная точка для множества точек шара 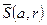, то есть докажем, что существует 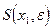, не содержащий точек

шара 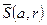. Построим 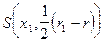. Будем доказывать методом от противного: пусть и пусть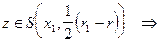

,

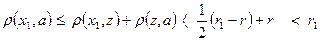что противоречит условию (1). Следовательно вне шара 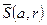нет предельных точек шара. Ч.Т.Д.

ТЕОРЕМА 2. Дополнение открытого множества до всего пространства всегда замкнутое. Дополнение замкнутого множества до всего пространства всегда открытое.

Доказательство:

Пусть F - замкнутое множество. Тогда U=CF - его дополнение до всего пространства. Докажем, что оно открытое.

Пусть 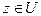. Допустим, что 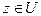без окрестности, т. е. в любом открытом шаре с центром в точке z существуют точки множества F. Тогда z - предельная точка множества F. Т.к. F - замкнутое множество, то 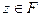, что противоречит условию 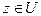. Следовательно, U - открытое множество.

Пусть теперь U - открытое множество, а F=CU - его дополнение до всего пространства. Докажем, что оно замкнутое.

Действительно, 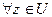вместе с некоторой окрестностью и поэтому не может быть предельной точкой множества F. Тогда все предельные точки множества F могут быть только в F. Следовательно, F - замкнутое множество

Ч.Т.Д.

Пример: Так как множество всех действительных чисел 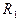(точек числовой оси) - замкнутое множество, то его дополнение С 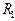= - открытое множество. Таким образом, из этого примера и примера п. 8.2 мы убедились, что является примером одновременно замкнутого множества и открытого.

Очевидно, это утверждение справедливо и для множества всех действительных чисел .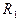

ТЕОРЕМА 3. Объединение замкнутых множеств в конечном числе и пересечение замкнутых множеств в любой совокупности есть замкнутое множество.

Доказательство:

Пусть 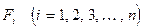- замкнутые множества, а 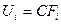- дополнительные открытые множества. Тогда из принципа двойственности имеем: 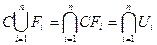- открытое множество по теореме 2 параграфа 6. Но тогда 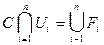- замкнутое множество по теореме о дополнениях.

Аналогично. 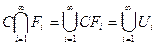- открытое множество по теореме 2 параграфа 6. 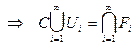- замкнутое множество по теореме о дополнениях. Ч.Т.Д.