Линейные пространства.

Определение. Линейным пространством L = {a, b, c, …} называется множество, относительно элементов которого определены операции сложения и умножения на число, причем результаты этих операций принадлежат этому же множеству (говорят, что L замкнуто относительно операций сложения и умножения на число): .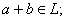

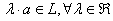(Элементы линейных пространств также будем называть векторами)

Для 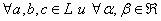эти операции удовлетворяют следующим условиям:

1. a + b = b + a (коммутативность сложения).

2. (a + b) + c = a + (b + c) (ассоциативность сложения).

3. .

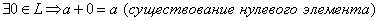4.

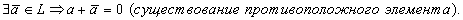
5. 1 ·а = а.

6.

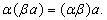
7. (α + β)а = α а + β а (дистрибутивность).

8. α (а + b) = α a + α b (дистрибутивность).

Перечисленные свойства, обычно, называют аксиомами. Имеют место теоремы:

Теорема 1. Нулевой элемент – единственен.

{От противного: 0₁, 0₂; 0₁+0₂=0₁ и 0₂+0₁=0₂ (акс. (3)). Из акс.(1) следует: 0₁=0₂}

Теорема 2. 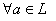противоположный элемент – единственен.

{Пусть для }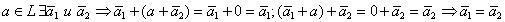

Теорема 3. 0 ·а = 0.

{ }

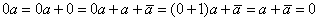Теорема 4.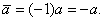

{ }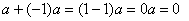