Гильбертовы пространства.

Определение 1. Полное унитарное пространство называется гильбертовым.

Пусть X — нормированное пространство. Замкнутое векторное пространство A ⊂ X называется подпро- странством X. Пусть E ⊂ X. Наименьшее линейное пространство L(E), содержашее E, называется линейной оболочкой множества E. Замыкание L(E) линейной оболочки множества E называется линейным замыканием E. Система элементов {xα } называется полной в пространстве X, если L({xα }) = X.

Теорема 1. (основная теорема гильбертова пространства)

Пусть H1 - подпространство H и H2 - его ортогональное дополнение. Тогда каждый x ∈ H единственным образом представим в виде

x = x’+x” (x‘∈ H1, x“∈ H2). (3)

При этом x‘ реализует расстояние от x до H1, т.е. ||x − x‘|| = ρ (x, H1). (4)

Доказательство. Положим d = ρ (x, H1), dn = d +1 n и для каждого n ∈ Nнайдем xn ∈ H1 такой, что

||x − xn|| < dn. (5)

В силу

||2x − (xn + xm)||²+ ||xm − xn||²= 2(||x − xn||²+ ||xm − x||²). (6)

Так как (xn+xm)/2∈ H1, то ||x –(xn+xm)/2||= > d или ||2x − (xn + xm)||² > 4d².

Тогда из (6) с помощью (5) находим

||xm − xn||²< = 2(d²n + d²m) − 4d².

Но dn, dm → d и потому ||xm − xn||n, m→ ∞ → 0, т.е. последовательность {xn} фундаментальная. Вследствие полноты H существует x‘ = lim xn, а так как множество H1 замкнуто (по определению подпространства), то x ‘∈ H1. При этом ||x − x‘|| = lim ||x − xn|| и из (5) следует, что ||x − x‘||< = d. Но так как знак " меньше" невозможен, то

||x − x‘|| = d. (7)

Теперь положим x“ = x − x‘ и покажем, что x“∈ H2, т.е. x“ ⊥ H1. Возьмем y ∈ H1 \ {θ }. При любом λ имеем x 0 + λ y ∈ H1, так что

4||x“− λ y||²= ||x − (x‘+ λ y)||²> d²,

что можно переписать, используя (7), в форме −

λ (x“, y) − λ (y, x“) + |λ |²(y, y) => 0.

В частности, при λ = (x“, y)/(y, y) получаем отсюда –

|(x“, y)|²/(y, y) − |(x“, y)|²/(y, y) + |(x“, y)|²/(y, y) > 0

, т.е. |(x“, y)|²< = 0, что может быть лишь в случае (x“, y) = 0. Итак, возможность представления x в форме (3) и соотношение (4) установлены.

Докажем единственность представления (3). В самом деле, если x =x‘1 +x“1(x‘1 ∈ H1, x“1 ∈ H2), то сопоставив это с (3) получим x‘ − x‘1 = x“1 − x“.

Поскольку x‘ − x‘1 ∈ H1, x“1 − x“ ∈ H2, то x‘ − x‘ 1 ⊥ x“ 1 − x“, откуда получаем

x‘ − x‘ 1 = x” 1 − x“ = θ.

Элементы x‘ и x‘’, однозначно определяемые элементом x, называются проекциями элемента x на пространство H1 и H2 соответственно.

Следствие 1. Для того, чтобы система элементов {xα }, (α ∈ ∆) была полной в пространстве H, необходимо и достаточно, чтобы не существовало отличного от θ элемента ортогонального каждому элементу системы.

Доказательство. Необходимость вытекает из предложения d). Если H1 = L({xα }) =/= H, т.е. система элементов {xα } не полна в H, то взяв x ∈ H|H1 и разложив его на сумму проекций x = x‘ + x“(x‘∈ H1, x“ ⊥ H1) будем иметь x“ =/= θ и x“ ⊥ xα (α ∈ ∆).

Примеры

Простейшим (но весьма важным) примером гильбертова пространства является пространство 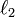. Его точки суть бесконечные последовательности действительных чисел 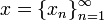, для которых сходится ряд 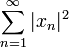. Скалярное произведение на этом пространстве задаётся равенством

.

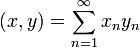Другим важным примером гильбертова пространства может служить пространство 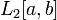измеримых функций на отрезке 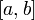с интегрируемыми по Лебегу квадратами — т. е. таких, что интеграл

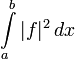
определён и конечен. Скалярное произведение на этом пространстве задаётся равенством

.
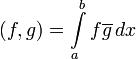