Линейные нормированные пространства.

Определение: пусть E – линейное пространство, 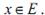Нормой эле-

мента x называется функция 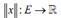: со свойствами (аксиомами нор-

мы):

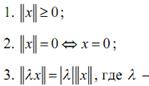действительное (комплексное) число;

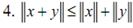– аксиома треугольника.

Линейное пространство E, на котором введена норма, называется ли-

нейным нормированным пространством.

Замечание: всякое нормированное пространство становится метриче-

ским, если в нем ввести расстояние по формуле 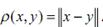. Справед-

ливость аксиом метрического пространства следует из аксиом нормы (см.

задачу 1). Таким образом, нормированные пространства обладают всеми

свойствами, установленными ранее для метрических пространств. Однако,

не каждое метрическое пространство может быть нормированным с нор-

мой, согласованной с метрикой.

Определение: линейное нормированное пространство называется ба-

наховым, если оно полно (относительно сходимости по метрике

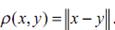, определяемой его нормой).

Определение: пусть E – линейное нормированное пространство,

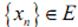– последовательность. Эта последовательность называется схо-

дящейся в пространстве E (сходящейся по норме пространства E) к эле-

менту , если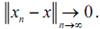

При этом обозначают 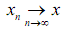или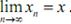

Теорема (о норме разности): пусть E – линейное пространство,

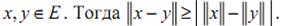. Тогда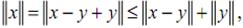

Доказательство: очевидно, что 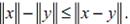, откуда

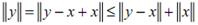. Аналогично, откуда 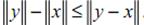. Учитывая, что 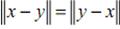, получаем требуемое.

Теорема доказана.

Теорема (простейшие свойства сходимости в нормированных про-

странствах): пусть E – линейное нормированное пространство,

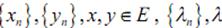– действительные (комплексные) числа, тогда:

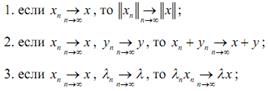
Доказательство:

1. Пусть

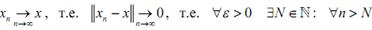. По теореме о норме разности

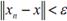, откуда следует, что, по определению предела числовой последовательности,

.

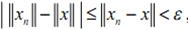2. Поскольку , то 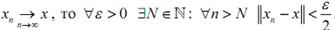 . Анало-

гично, поскольку

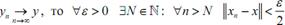. Тогда

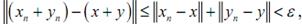, значит,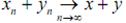

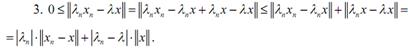Поскольку

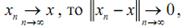, и, аналогично, поскольку

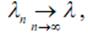то 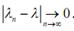. Кроме того, в силу необходимого условия существования

предела числовой последовательности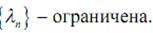

Переходя в неравенстве к пределу при , по теореме о двух ми-

лиционерах, получаем, что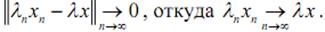

4., 5. См. задачу 4.

Теорема доказана.

Определение: два линейных нормированных пространства E1

и E2

называются изоморфными, если существует взаимно однозначное и вза-

имно непрерывное изоморфное отображение E1 на E2.

Теорема (об изоморфности конечномерных пространств): все ко-

нечномерные линейные нормированные пространства данного числа изме-

рений n изоморфны евклидову n –мерному пространству и, следова-

тельно, изоморфны друг другу.

Доказательство: пусть E – n –мерное линейное нормированное про-

странство и 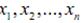– его базис, тогда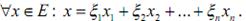

Поставим элементу в соответствие элемент

т.е. найдем отображение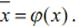

Ясно, что такое соответствие взаимно однозначно (по определению

базиса конечномерного пространства). Кроме того, при таком соответст-

вии, очевидно, сохраняются алгебраические операции, т.е. оно изоморфно.

Осталось показать, что введенное соответствие взаимно непрерывно, т.е.,

что из непрерывности 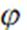по норме пространства 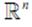следует непрерыв-

ность 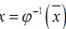по норме пространства E и наоборот.

Заметим, что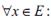

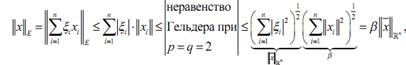откуда, очевидно, что

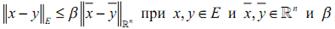, не

зависящим от x и y. Таким образом, из непрерывности по норме про-

странства 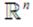следует непрерывность по норме пространства E. Осталось

получить противоположное неравенство.

Рассмотрим в пространстве единичную сферу

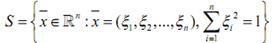и на ней рассмотрим функцию

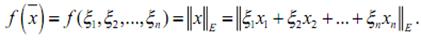Поскольку на S все 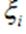не могут одновременно обратиться в 0, а вектора 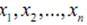линейно независимы, то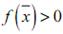

Далее, 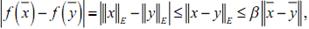, значит f равно-

мерно непрерывна, т.е. тем более непрерывна.

Поскольку – замкнутое и ограниченное множество, то это

компакт и по теореме Вейерштрасса f достигает на S своего наименьше-

го значения 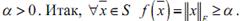Берем теперь 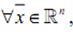, тогда

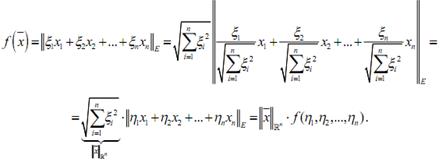Поскольку

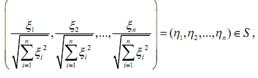, то

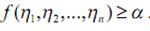Итак 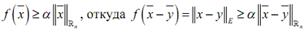Теорема доказана.

Определение: пусть E – линейное нормированное пространство, на

котором заданы две нормы 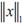и 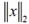.Норма 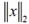называется подчиненной

норме 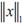, если 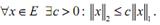

Теорема (о подчиненных нормах): пусть E – линейное нормирован-

ное пространство, на котором заданы две нормы 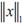и 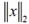.Пусть после-

довательность 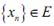сходится по норме 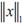.Тогда, если 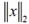подчинена 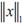, то последовательность 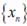сходится и по норме 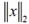, причем к тому

же пределу.

Доказательство: пусть 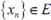сходится к по норме 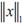, т.е. 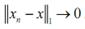. По определению подчиненных норм 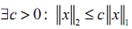Переходя к пределу при 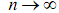, по теореме о двух милиционерах, получаем, что 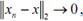, что и означает сходимость последовательности 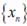по норме 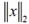к тому же самому пределу .

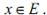Теорема доказана.

Определение: пусть E – линейное нормированное пространство, на

котором заданы две нормы 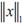и 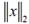.Эти нормы называются эквивалент-

ными, если 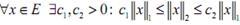

Замечание: если две нормы эквивалентны, то сходимость по любой

из них влечет сходимость по другой (см. задачу 5).

Следующее утверждение, полезное при решении некоторых задач,

примем пока без доказательства.

Теорема (об эквивалентных нормах): пусть E – линейное нормиро-

ванное пространство, на котором заданы две нормы 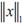и 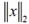, по отноше-

нию к каждой из которых пространство E – банахово. Если хотя бы одна

из норм подчинена другой, то эти нормы эквивалентны.