Теорема Шаудера.

Рассмотрим уравнение 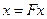с непрерывным оператором .

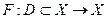Теорема Шаудера. Пусть 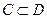- непустое замкнутое выпуклое множество. Если выполнены условия:

1. ;

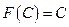2. 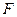- вполне непрерывный оператор;

Следовательно, существует хотя бы одна неподвижная точка оператора .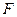

Примем теорему без доказательства.

На практике часто возникает необходимость построения выпуклого множества 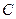. Рассмотрим утверждение (следствие теоремы Шаудера), в котором в качестве 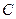выступает замкнутый шар с центром в 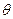и некоторого радиуса .

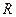Следствие. Пусть вполне непрерывный оператор 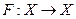удовлетворяет неравенству

, ,

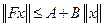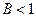следовательно, существует хотя бы одна неподвижная точка.

Неравенство в следствии является ограничением на скорость роста нелинейного оператора 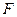. Кроме того, это неравенство является аналогом условия Липшица на бесконечности.

Для доказательства достаточно в силу теоремы Шаудера проверить, что неравенство обеспечивает существование такого замкнутого шара 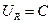, такой что: .

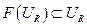Зафиксируем радиус шара 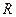и рассмотрим неравенство

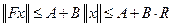, где .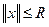

Это неравенство означает, что

,

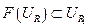где 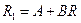. Если 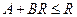, то 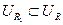, следовательно, для данного радиуса выполняется требуемое вложение .

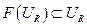Рассмотрим зависимость 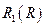. Пусть существует 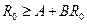, следовательно, для данного радиуса выполняется 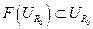, следовательно, выполняются все условия теоремы Шаудера, то есть, вместе с вполне непрерывностью оператор 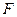отражает непустое выпуклое замкнутое множество в себя 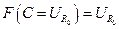, следовательно, существует хотя бы одно решение системы (1), то есть, существует неподвижная точка.

Следствие и теорема гарантируют существование неподвижной точки, но не обеспечивают её единственность.

Задача Коши для обыкновенного дифференциального уравнения первого порядка.

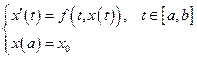
Функция непрерывна. Как было показано, разрешимость данной задачи следует из разрешимости интегрального уравнения:

,

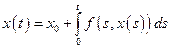которое представим в виде операторного уравнения 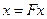, 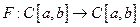. Всякое непрерывное решение интегрального уравнения является непрерывным решением дифференциального уравнения задачи Коши.

Для доказательства существования неподвижной точки оператора 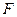(а это в конечном счете означает, что задача Коши имеет хотя бы одно решение) воспользуемся утверждением следствия. Отметим, что из непрерывности функции двух переменных следует вполне непрерывность оператора 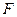. Доказательство этого факта проводится с применением теоремы Арцела по той же схеме, что и доказательство вполне непрерывности интегрального оператора. Для доказательства существования неподвижной точки остается обеспечить выполнение неравенства в следствии. Для этого предположим, что функция 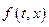удовлетворяет неравенству:

,

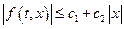Имеем

,

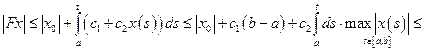
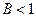
Теорема. Пусть выполнены условия:

1. 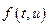непрерывная функция;

2. выполняется ;

3. ,

следовательно, задача Коши имеет хотя бы одно значение.

Отметим, что в этой теореме, как и в теореме о существовании единственности важное значение имеет произведение длин отрезков на константу 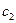, поэтому в теории дифференциальных уравнений для данной задачи, что бы достичь условия существования или единственности регулируют длину промежутка. Такие утверждения называют локальными в отличии от полученных в данной главе глобальных.

Отметим, что теоремы существования и существования единственности остаются, справедливы и при более слабых ограничениях на функцию двух переменных. Например, необязательно непрерывность 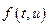по переменной .,