
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Распределение Стьюдента.
|
|
Пусть Х1, Х2, …, Хn нормально распределенные случайные величины, m=0, σ =1.
Тогда СВ 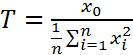 – соотношение Стьюдента. А ее распределение – распределение Стьюдента с ν =n степенями свободы.
– соотношение Стьюдента. А ее распределение – распределение Стьюдента с ν =n степенями свободы.
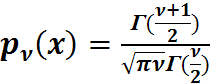
Замечание. СВ Т часто записывают 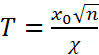 где
где 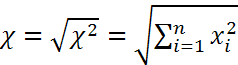 .
.
График плотности:
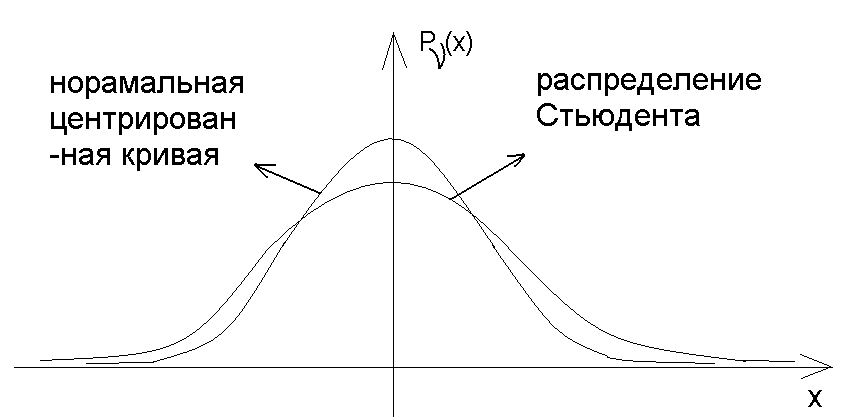 Внешне напоминает график плотности нормального стандартного распределения. При больших ν график
Внешне напоминает график плотности нормального стандартного распределения. При больших ν график 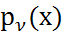 центрирован нормальной кривой (т.е. m=0, σ =1). Составлена таблица
центрирован нормальной кривой (т.е. m=0, σ =1). Составлена таблица 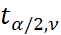
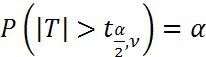 . Построим график: S1+S2=α (α -заданный) уровень вероятности,
. Построим график: S1+S2=α (α -заданный) уровень вероятности, 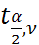 - квантили распределения Стьюдента.
- квантили распределения Стьюдента. 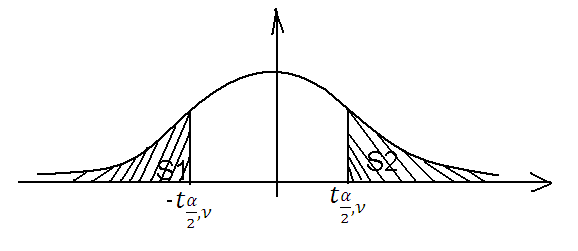
41. Доверительный интервал для мат. ожидания нормально распределенной С.В.( 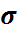 -неизвестно)
-неизвестно)
Опр. Доверительным интервалом для параметра 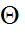 наз-ся интервал (обозн.
наз-ся интервал (обозн. 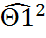 ,
, 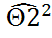 ), содержащий (накрывающий) истинное значение неизвестного параметра
), содержащий (накрывающий) истинное значение неизвестного параметра 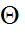 с заданной вероятностью p=1-
с заданной вероятностью p=1- 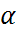
Опр: Число 1- 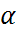 наз-ся доверительной вероятностью.
наз-ся доверительной вероятностью.
Постановка задачи: Пусть наблюдается нормальное распределение С.В. Х.произведена выборка обьема n.Требуется найти доверительный интервал с заданной доверительной вероятностью 1- 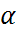 для мат. ожидания m С.В. Х
для мат. ожидания m С.В. Х
Для этого найдем такое 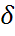 > 0, что P(
> 0, что P(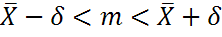 )= 1-
)= 1- 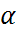 (**)
(**)
Ищем 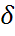 , чтоб вып-ось это равенство
, чтоб вып-ось это равенство
P(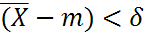 )= 1-
)= 1- 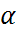 (**)
(**)
1)Пусть 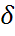 неизвестна, т.е.
неизвестна, т.е. 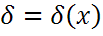 .В силу Теоремы2 из пункта распределение Стьюдента С.В.
.В силу Теоремы2 из пункта распределение Стьюдента С.В.
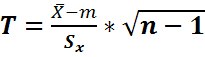 , где
, где 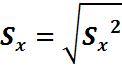 - выбор среднего квадратичного отклонения имеет распределение Стьюдента с
- выбор среднего квадратичного отклонения имеет распределение Стьюдента с 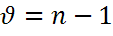 степенями свободы
степенями свободы
Т.к. 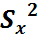 =
= 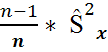 следовательно
следовательно 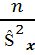 =
= 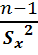
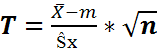 - распределение по Стьюденту с
- распределение по Стьюденту с 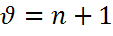 степенями свободы
степенями свободы
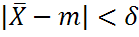
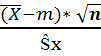 <
< 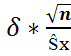
Ищем 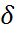 чтобы: P(
чтобы: P(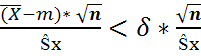 )= 1-
)= 1- 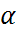
P(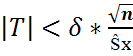 )= 1-
)= 1- 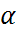
P(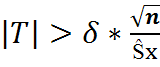 )=
)= 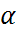
По таблице находим такое значение 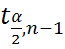 что P(
что P(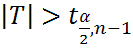 )=
)= 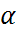 , Тогда
, Тогда 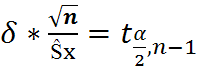 следовательно
следовательно 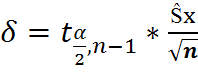
Тогда искомый доверительный интервал 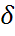 будет иметь вид
будет иметь вид
(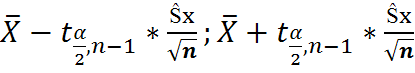 )
)
40. Доверительный интервал для мат. ожидания нормально распределенной С.В.( 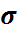 -известно)
-известно)
Опр. Доверительным интервалом для параметра 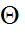 наз-ся интервал (обозн.
наз-ся интервал (обозн. 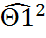 ,
, 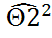 ), содержащий (накрывающий) истинное значение неизвестного параметра
), содержащий (накрывающий) истинное значение неизвестного параметра 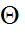 с заданной вероятностью p=1-
с заданной вероятностью p=1- 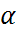
Опр: Число 1- 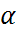 наз-ся доверительной вероятностью.
наз-ся доверительной вероятностью.
Постановка задачи: Пусть наблюдается нормальное распределение С.В. Х.произведена выборка обьема n.Требуется найти доверительный интервал с заданной доверительной вероятностью 1- 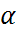 для мат. ожидания m С.В. Х
для мат. ожидания m С.В. Х
1)Пусть 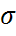 известно, т.е.
известно, т.е. 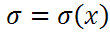 .
. 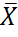 распределена нормально с параметрами m и
распределена нормально с параметрами m и 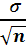
Тогда 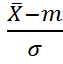 *
* 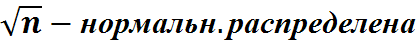 с параметрами
с параметрами  0 и 1.
0 и 1.
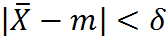
P(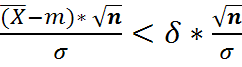 )= 1-α
)= 1-α
P(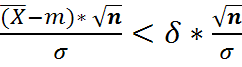 )=2
)=2 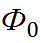 (
(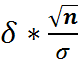 )
) 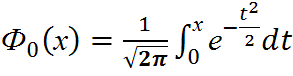
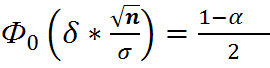
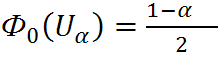 -Находим по таблице
-Находим по таблице 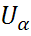
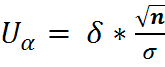 следовательно
следовательно 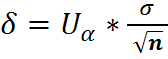
Т.О. искомый доверительный интервал имеет вид:
(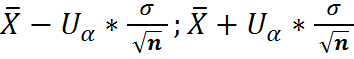 )
)
Замечание: U из формул 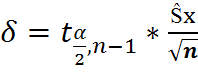 и
и 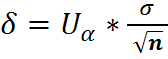 следует что с увеличением n точность оценки возрастает.
следует что с увеличением n точность оценки возрастает.