Означення похідної

ЛЕКЦІЯ 5-6. ПОХІДНА ФУНКЦІЇ

ПЛАН

1. Означення похідної

2. Геометричний зміст похідної

3. Механічний зміст похідної

4. Рівняння дотичної і нормалі до плоскої кривої

5. Залежність між неперервністю і диференційованістю функції

6. Основні правила диференціювання

7. Похідні від основних елементарних функцій

8. Похідні вищих порядків

Означення похідної

Нехай функція 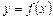визначена на деякому проміжку (а; b). Візьмемо значення 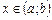і надамо аргументу приросту 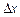. Тоді функція набуде приросту 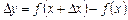. Розглянемо відношення приросту функції 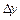до приросту аргументу 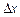і перейдемо до границі при :

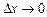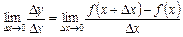. (1)

Якщо границя (1) існує і скінченна, вона називається похідною функції 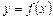за змінною х і позначається

.

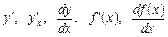Означення 1. Похідною функції 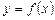за аргументом х називається границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля.

Операція знаходження похідної називається диференціюванням цієї функції.

Користуючись означенням похідної, знайти похідні функцій.

Приклад. Функція у = х ². Знайти похідну в точках х = 3 і х = – 4.

Надамо аргументу х приросту 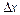, тоді функція набуде приросту

Складемо відношення приросту функції до приросту аргументу 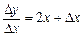, відшукаємо границю 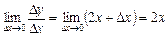. Таким чином, .

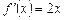Похідна в точці х = 3 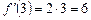, а похідна при х = – 4 буде .

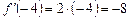Приклад. 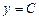, де .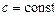

Надавши аргументу 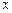приросту 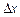, дістанемо приріст функ­ції 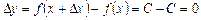. Тепер знайдемо границю відношення 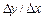при :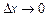

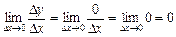, тобто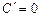

Приклад. .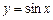

Користуючись відомою з тригонометрії формулою

,

знайдемо приріст функції у точці 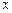і обчислимо границю:

,

;

.

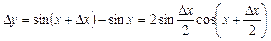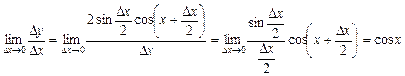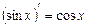Аналогічно можна дістати: .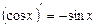

Приклад. .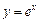

Для цієї функції маємо

,

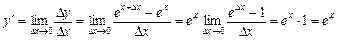тобто 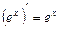.