Теорема. Якщо функція диференційована в деякій точці, то у цій точці функція неперервна.

Обернене твердження неправильне: для неперервної функції може не існувати похідної.

Справді, нехай функція 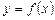диференційована в точці 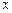. Запишемо тотожність , звідси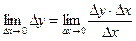

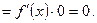
Таким чином, функція 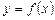неперервна в точці .

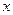Наслідок. Якщо функція розривна в деякій точці, то вона не має похідної в цій точці.

Прикладом неперервної функції, що не має похідної в одній точці, є функція 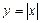(рис.5). Ця функція неперервна при х = 0, але не диференційована для цього значення, оскільки в точці з абсцисою х = 0 не існує дотичної до графіка функції.

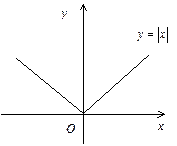Рис. 5

Таким чином, необхідною умовою диференційованості функції у = f (х) у точці х є її неперервність у цій точці.

Основні правила диференціювання

Теорема 1. Похідна сталої дорівнює нулю, тобто якщо у = с, де с = const, то 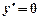.