
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Похідні від основних елементарних функцій
|
|
За аналогією з попередніми прикладами можна дістати похідні від основних елементарних функцій:
1. 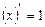 ; 2.
; 2. 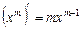 ;
;
3. 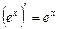 ; 4.
; 4. 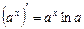 ;
;
5. 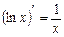 ; 6.
; 6.  ;
;
7. 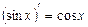 ; 8.
; 8. 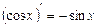 ;
;
9. 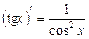 ; 10.
; 10. 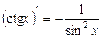 ;
;
11. 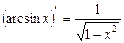 ; 12.
; 12. 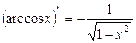 ;
;
13. 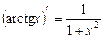 ; 14.
; 14. 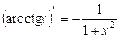 .
.
Продиференціювати подані далі функції.
Приклад. 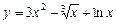 .
.
l Дана функція є алгебраїчною сумою функцій, тому використовуємо теорему 2:
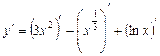 .
.
У здобутому виразі перший доданок алгебраїчної суми є добуток сталої величини на степеневу функцію Þ — застосуємо до нього теорему 4 і формулу (2) таблиці похідних; другий — ірраціональна функція з показником 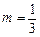 — застосуємо формулу (2) таблиці похідних; третій — логарифмічна функція з основою е Þ — використаємо формулу (5):
— застосуємо формулу (2) таблиці похідних; третій — логарифмічна функція з основою е Þ — використаємо формулу (5):
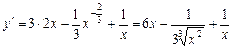 .
.
Приклад. 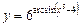 .
.
Задана функція складна: зовнішня — показникова функція з основою 6, внутрішня для неї — обернена тригонометрична. Обернена тригонометрична, у свою чергу, є складною, для якої внутрішня функція — алгебраїчна сума 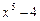 . Для суми аргументом (скінченним) є х.
. Для суми аргументом (скінченним) є х.
Таким чином, задана функція є суперпозицією трьох функцій.
При диференціюванні послідовно застосовуємо два рази теорему 6:
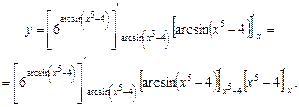
У цьому виразі знизу біля кожної квадратної дужки вказано аргумент, за яким слід диференціювати функцію, взяту в дужки.
Тепер послідовно скористаємося формулами (4), (11), (2) таблиці похідних та теоремами 1, 2. Дістанемо:
 .
.
Взагалі використані правила та формули не фіксують, а записують кінцевий результат їх застосування.
Приклад. 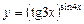 .
.
Задана функція є степенево-показниковим виразом виду
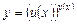 , де
, де 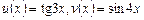 . (5)
. (5)
Прологарифмуємо функцію (4.5) за основою е:
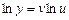 . (6)
. (6)
Оскільки 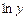 і
і 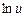 — складні функції, після диференціювання обох частин рівності (4.6) дістанемо:
— складні функції, після диференціювання обох частин рівності (4.6) дістанемо:
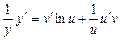 .
.
Звідси 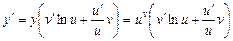 .
.
Таким чином, дістали формулу для знаходження похідної від степенево-показникової функції виду (4.5).
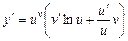 . (7)
. (7)
У даному випадку формула (7) виглядає як
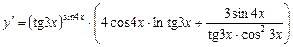 .
.