Застосування деференціала в наближених обчисленнях

Вираз (2) з урахуванням (3) можна записати так:

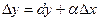. (4)

Якщо 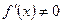, то величина 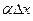є малою величиною вищого порядку порівняно з dy.

При малих 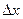доданком 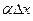у виразі (4) нехтують і користуються наближеною рівністю 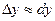, або в розгорнутому вигляді: 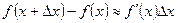, звідки

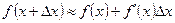. (5)

Остання наближена рівність тим точніша, чим менше .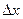

Приклад. Обчислити наближено .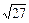

Перетворимо вираз, що стоїть під знаком радикала:

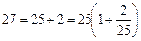, звідки 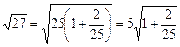. (6)

При обчисленні 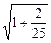введемо функцію 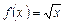, тоді .

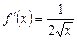Формула (5) у нашому випадку запишеться так:

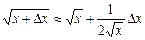, де .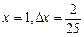

Інакше

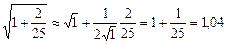. (7)

Підставивши (7) у рівність (6), дістанемо

.

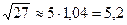Правила знаходження диференціала

Застосовуючи формулу похідної та властивості похідних, дістаємо правила знаходження диференціала:

1. у = с; dy = 0; 3.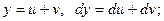

2. 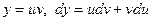; 4. .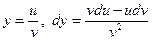

Теорема. Форма диференціала не залежить від того, чи є аргумент незалежною змінною або функцією.