Основні теореми диференціального числення

Теорема Ферма. Якщо диференційовна на проміжку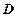
функція 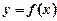досягає найбільшого або найменшого значення у внутрішній точці 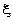цього проміжку, то похідна функції в цій точці дорівнює нулю, тобто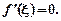

Припустимо, для визначеності, що 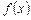набуває в точці 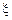найбільшого значення, тобто для всіх .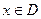

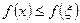За означенням похідної

,

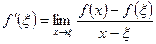причому ця границя не залежить від того, як наближається 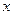до 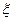— справа чи зліва.

Розглянемо відношення .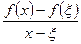

Для всіх х, достатньо близьких до точки 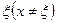, маємо:

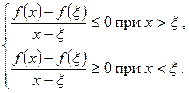
Перейдемо в останніх нерівностях до границі при 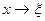. Дістанемо

.

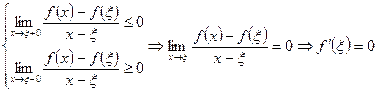Аналогічно розглядається випадок, коли функція 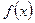набуває в точці 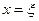найменшого значення.

Геометричний зміст теореми Ферма. Геометричний зміст похідної 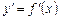являє собою кутовий коефіцієнт дотичної до кривої 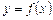. Звідси рівність нулю похідної 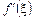геометрично озна­чає, що у відповідній точці цієї кривої дотична паралельна осі Ох.

Теорема Ролля. Якщо функція f (х): 1) неперервна на сегменті [ a; b ]; 2) диференційовна на інтервалі (а; b); 3) на кінцях сегмента набуває рівних між собою значень, тобто f (a) = f (b), то на інтервалі (а; b) існує хоча б одна точка 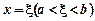, для якої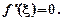

Геометричний зміст теореми Ролля. Якщо крайні ординати неперервної кривої у = f (х), яка має в кожній точці дотичну, рівні, то на цій кривій знайдеться принаймні одна точка з абсцисою 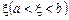, в якій дотична паралельна осі Ох (рис. 6).

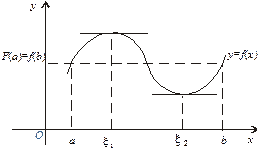
Рис. 6