Означення диференціалу функції

ЛЕКЦІЯ 7. ДИФЕРЕНЦІАЛ ФУНКЦІЇ ОДНІЄЇ ЗМІННОЇ. Основні теореми диференціального числення

ПЛАН

1. Означення диференціалу функції

2. Застосування деференціала в наближених обчисленнях

3. Правила знаходження диференціала

4. Основні теореми диференціального числення

Означення диференціалу функції

Нехай функція у = f (х) диференційовна на деякому проміжку, тобто для будь-якої точки х з цього проміжку границя 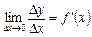існує і дорівнює скінченному числу.

Враховуючи взаємозв’язок змінної величини, що має скінченну границю, і нескінченної малої величини, можемо записати 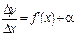, де 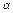— нескінченно мала величина ( 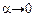при ).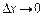

Помноживши всі члени останньої рівності на 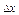, дістанемо

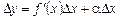. (1)

З виразу (1) випливає, що приріст функції складається із суми двох доданків, з яких перший доданок — так звана головна частина приросту, лінійна відносно 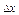(при 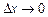добуток 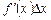є нескінченно мала величина першого порядку відносно 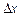). Другий доданок — добуток 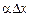завжди нескінченно мала величина вищого порядку, ніж .

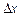Означення 1. Добуток 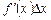називається диференціалом функції у = f (х); його позначають символом dy, тобто

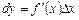(2)

Знайдемо диференціал функції у = х; для цього випадку , отже, 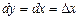. Таким чином, диференціал незалежної змінної збігається з її приростом 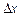. З огляду на це формулу для диференціала (2) можна записати так:

. (3)

Приклад. Знайти диференціал dy функції 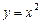: 1) при довільних значеннях х та 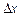; 2) при х = 20, 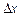= 0, 1.

1) ;

2) якщо х = 20, 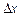= 0, 1, то .

Приклад. Знайти диференціал dy функції .

Оскільки , то за формулою (3) дістанемо

.
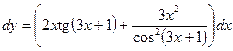