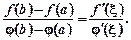Теорема Лагранжа (теорема про скінченні прирости функції).

Якщо функція f (х): 1) неперервна на сегменті [a; b]; 2) диференційовна на інтервалі (а; b), то на інтервалі знайдеться хоча б одна точка, така що

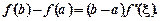(8)

Геометричний зміст теореми Лагранжа. Запишемо формулу (8) у вигляді

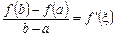. (9)

З рис. 4.7 бачимо, що величина 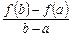є тангенсом кута 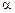нахилу хорди, що проходить через точки А і В графіка функції
у = f (х) з абсцисами а і b.

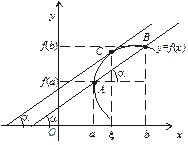
Рис. 7

Водночас, 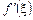— тангенс кута нахилу дотичної до кривої у точці С з абсцисою 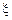. Таким чином, геометричний зміст рівності (8) або рівносильної для неї рівності (9) можна визначити так: якщо для всіх точок кривої у = f (х) існує дотична, то на цій кривій знайдеться точка з абсцисою 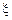, в якій дотична паралельна хорді АВ, що сполучає точки А і В.

Теорема Коші. Якщо f (x) і дві функції: 1) неперервні на сегменті [a; b]; 2) диференційовні на інтервалі (а; b); 3) для, то на інтервалі (а; b) знайдеться хоча б одна точка, така що