Перетворення невизначеностей виду

ПЛАН

1. Правило Лопіталя

2. Перетворення невизначеностей виду

3. Зростання та спадання функцій

4. Екстремуми функцій

5. Найбільше і найменше значення функції на відрізку

1. Правило Лопіталя

Розглянемо відношення 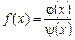, де функці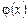ї і 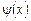визначені й диференційовні в деякому околі точки а, виключаючи, можливо, саму точку а. Може бути, що при 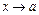обидві функці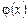ї і 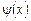прямують до 0 або до ¥, тобто ці функції одночасно є нескінченно малими або нескінченно великими величинами при 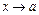. Тоді говорять, що в точці а функція f (x) має невизначеність виду

.

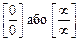У цьому випадку, використовуючи похідн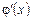і і 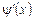, можна сформулювати правило для знаходження границі функції f (x) при 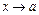, тобто визначити спосіб для розкриття невизначеностей виду .

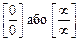Теорема (правило Лопіталя). Границя відношення двох нескінченно малих або нескінченно великих функцій дорівнює границі відношення їхніх похідних (скінченній або нескінченній), якщо остання існує.

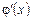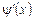Зауваження. Якщо і при 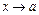прямують одночасно до 0 або до ¥ і задовольняють ті умови, які були накладені теоремою на функці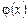ї і 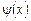, то до відношення 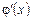/ 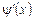знову застосовуємо правило Лопіталя і виводимо формулу

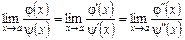
і т. п.

Приклад. Знайти .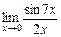

Виконавши граничний перехід, дістанемо невизначеність вигляду 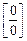. Застосовуємо правило Лопіталя:

.

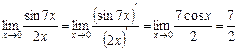Приклад. Знайти .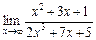

Виконання граничного переходу приводить до невизначеності виду 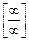. Застосовуємо правило Лопіталя:

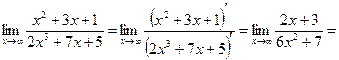
(виконання граничного переходу знову приводить до невизначеності виду 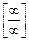, а тому застосовуємо правило Лопіталя повторно):

.

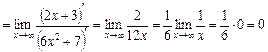Перетворення невизначеностей виду

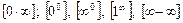до виду 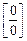або .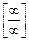

Правило Лопіталя можна застосувати тільки для розкриття невизначеностей вигляду 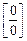або 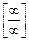. При розкритті інших типів невизначеностей їх перетворюють до одного з цих видів.

Невизначеність виду . Нехай .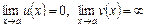

Потрібно знайти

.

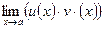Це невизначеність типу .

Якщо вираз 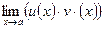записати у вигляді

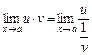або ,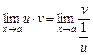

то при 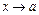дістанемо невизначеність відповідно вигляду 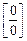або .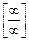

Приклад. Знайти .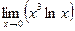

Тут маємо невизначеність вигляду 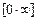. Зобразимо добуток функції у вигляді частки, а потім, отримавши невизначеність 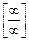, застосуємо правило Лопіталя:

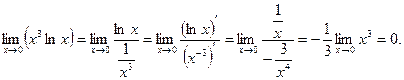
Невизначеність вигляду 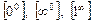. Нехай маємо функцію .

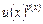При 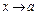(а — скінченне або нескінченне) можливі три випадки:

а) маємо невизначеність виду ;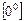

б) 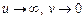дістанемо невизначеність ;

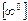в) 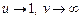маємо невизначеність виду .

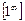Ці невизначеності за допомогою логарифмування зводяться до невизначеності вигляду 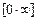. Справді, позначимо дану функцію через у, тобто візьмемо 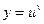. Прологарифмувавши цю рівність, дістанемо .

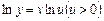Легко перевірити, що при 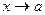добуток 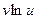буде невизначеністю для всіх трьох випадків.

Відповідно до пункту 1 розкриємо невизначеність 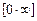, тобто знайдемо границю 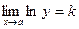(k — скінченне або ¥).

Звідси .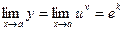

Приклад. Знайти границю .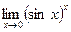

Це невизначеність виду 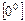. Позначимо функцію, що стоїть під знаком границі, через у, тобто 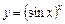, і прологарифмуємо її:

.

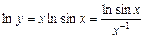Обчислимо границю логарифма даної функції. Тут маємо невизначеність 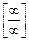. Застосуємо правило Лопіталя:

.

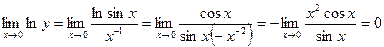Звідси .

Приклад. Знайти границю .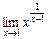

При 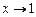маємо невизначеність .

.

Звідси .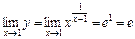

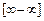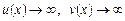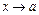Невизначеність . Якщо функції при (а — скінченне або нескінченне), то різниця 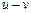при 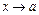дає невизначеність 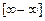. Остання з допомогою алгебраїч­них перетворень зводиться до невизначеності 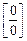або .

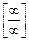Приклад. Знайти границю .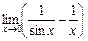

Маємо невизначеність виду 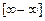. Алгебраїчним перетворенням приведемо цю невизначеність до невизначеності 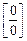, а потім двічі застосуємо правило Лопіталя:

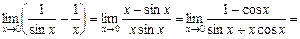
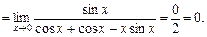
3. Зростання та спадання функцій

Нагадаємо: функція f (x) називається зростаючою на проміжку, якщо більшому значенню аргументу відповідає більше значення функції (якщо то ); функція спадна на проміжку, якщо більшому значенню аргументу відповідає менше значення функції (якщо , то ).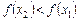

Теорема 1 (необхідна умова зростання (спадання) функції):

1. Якщо диференційовна функція зростає на деякому проміжку, то похідна цієї функції невід’ємна на цьому проміжку.

2. Якщо диференційовна функція спадає на деякому проміжку, то похідна цієї функції недодатна на цьому проміжку.

Теорема 2 (достатня умова зростання (спадання) функції):

1. Якщо похідна диференційовної функції додатна всередині деякого проміжку, то функція зростає на цьому проміжку.

2. Якщо похідна диференційовної функції від’ємна всередині проміжку, то функція спадає на цьому проміжку.

Приклад. Знайти проміжки зростання та спадання функції .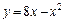

Область визначення функції — уся числова вісь 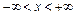. Знайдемо похідну 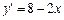. Функція диференційовна на проміжку .

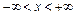Для визначення проміжку зростання функції розв’яжемо нерівність 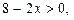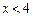, тобто функція зростає на проміжку .

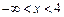При визначенні проміжку спадання функції (рис. 4.8) маємо 8 – 2 х < 0, тобто .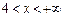

4. Екстремуми функцій

Означення. При значенні х ₁ аргументу х функція f (х) має максимум f (х ₁), якщо в деякому околі точки х ₁ виконується нерівність (рис. 1) 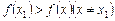. Аналогічно: при значенні х ₂ аргументу х функція f (х) має мінімум f (х ₂), якщо в деякому околі точки х ₂ має місце нерівність (див. рис. 4.9) .

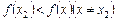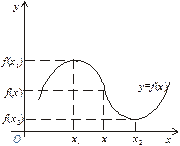
Рис. 1

Максимум або мінімум функції називається екстремумом функції, а ті значення аргументу, при яких досягаються екстремуми функції, називаються точками екстремуму функції (відповідно точками максимуму або мінімуму функції).

Екстремум функції, у загальному випадку, має локальний характер — це найбільше або найменше значення функції порівняно з ближніми її значеннями.

Необхідна умова екстремуму функції. Теорема. У точці екстремуму диференційовної функції похідна її дорівнює нулю:

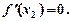
Геометрична умова 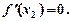означає, що в точці екстремуму диференційовної функції 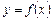дотична до її графіка паралельна осі Ох (рис. 2).

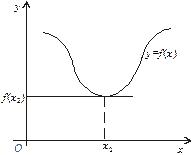
Рис. 2

Наслідок. Неперервна функція може мати екстремум тільки в тих точках, де похідна функції дорівнює нулю або не існує.

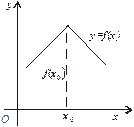Рис. 3

Справді, якщо в точці х ₀ екстремуму функції 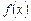існує похідна 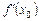, то, згідно з даною теоремою, ця похідна дорівнює нулю.

Те, що в точці екстремуму неперервної функції похідна може не існувати, показує приклад функції, графік якої має форму «ламаної» (рис. 3).

Ті значення аргументу х, які для заданої функції перетворюють на нуль її похідну 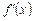або для якої похідна 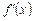не існує (наприклад, перетворюється на нескінченність), називаються критичними значеннями аргументу (критичними точками).

Достатні умови екстремуму функції. Із того, що 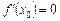, не випливає, що функція 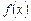має екстремум при .

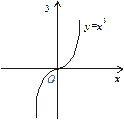Рис. 4

Наприклад, нехай 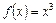. Тод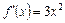і і 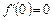, однак значення 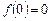не є екстремумом даної функції, оскільки різниця 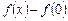змінює знак при зміні знаку аргументу х (рис. 4).

Отже, не для будь-якого критичного значення аргументу функції 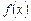має місце екстремум цієї функції. Через це поряд з необхідною умовою існують достатні умови існу­вання екстремуму функції.