Теорема 7. Похідна оберненої функції по змінній у дорівнює оберненій величині похідної від прямої функції .

Приклад. Обчислити похідну для функції .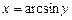

Задана функція обернена до функції .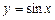

Згідно з теоремою 7 можна записати

.

Звідси .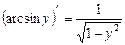

Якщо в останньому виразі замість у записати х, то дістанемо

.

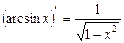Похідна параметрично заданої функції. Нехай функцію 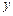від 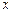задано параметричними рівняннями:

.

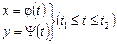Припустимо, що функції мають похідні і що функція 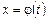має обернену функцію 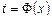, яка також є диференційовною. Тоді визначену параметричними рівняннями функціональну залежність 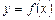можна розглядати як складну функцію 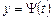, 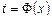( 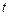— проміжний аргумент).

На підставі теорем 6 та 7 маємо:

, .

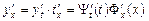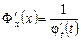Звідки 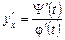або .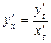

Знайдена формула дає можливість знаходити похідну 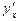від параметрично заданої функції, не знаходячи явної залежності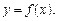

Приклад. Функцію 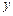від 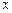задано параметричними рівняннями:

.

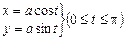Знайти похідну 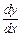: а) при будь-якому 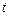; б) при .

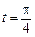а) ;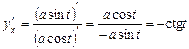

б) 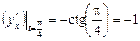.