Рівняння дотичної і нормалі до плоскої кривої

Нехай функція у = f (t) означена і неперервна на деякому проміжку [ a; b ]. Визначимо рівняння дотичної й нормалі до графіка функції у = f (x) у точці з абсцисою .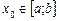

Оскільки дотична й нормаль проходять через точку з абсцисою х ₀, то рівняння кожної з них будемо шукати у вигляді рівняння прямої, що проходить через задану точку М ₀ (х ₀; у ₀) у даному напрямі (рис. 4):

, (2)

де k кутовий коефіцієнт дотичної. Використовуючи геометричний зміст похідної, маємо .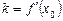

Рис. 4

Рівняння дотичної. Оскільки 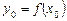, то з виразу (2) дістанемо рівняння дотичної у вигляді

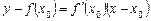. (3)

Рівняння нормалі. Означення. Нормаллю до графіка функції в точці М ₀ називається перпендикуляр, проведений до дотичної в цій точці (рис. 4).

Використовуючи умову перпендикулярності дотичної та нормалі, знаходимо кутовий коефіцієнт нормалі 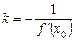і записуємо її рівняння у вигляді

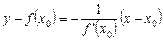. (4)

Приклад. Знайти рівняння дотичної та нормалі до графіка функції у = х ² у точці з абсцисою х ₀=–3.

Знайдемо похідну від заданої функції 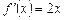, звідси .

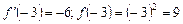Рівняння дотичної (3) і нормалі (4) запишуться так: 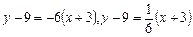або у загальному вигляді: 6 х + у +9=0, х –6 у +57=0.