Мультилинейная модель с кинематическим упрочнением

В этой модели материал представляется в виде последовательности нескольких частей (подъобъемов). Полные деформации всех частей одинаковы, но каждый подъобъем имеет свой собственный предел текучести. (Для пслоско-напряженного состояния принимается материал состоящий из нескольких слоёв, каждый из которых имеет свою толщину и предел текучести). Для каждого подъобъема принимается простая зависимость между напряжениями и деформациями, но их объединение позволяет получить комплексное сложное поведение, показанное на рисунке 4.1 б.

Для расчета пластики необходимо выполнить следующие шаги:

1. Определяется часть общего объема, выделяемая в подъобъём, и соответствующий ей предел текучести.

2. Рассчитывается приращение пластических деформаций для каждого подъобъема, исходя из предположения, что суммарные деформации одинаковы.

3. Отдельные приращения пластических деформаций суммируются с учетом весовых коэффициентов, определяемых на шаге 1, для получения полного приращения пластических деформаций.

4. Пересчитываются пластические деформации и вычисляются упругие деформации.

Части полного объема (весовой коэффициент) и пределы текучести для каждого подъобъема определяются в соответствии с кривой поведения материала (рисунок 4.5).

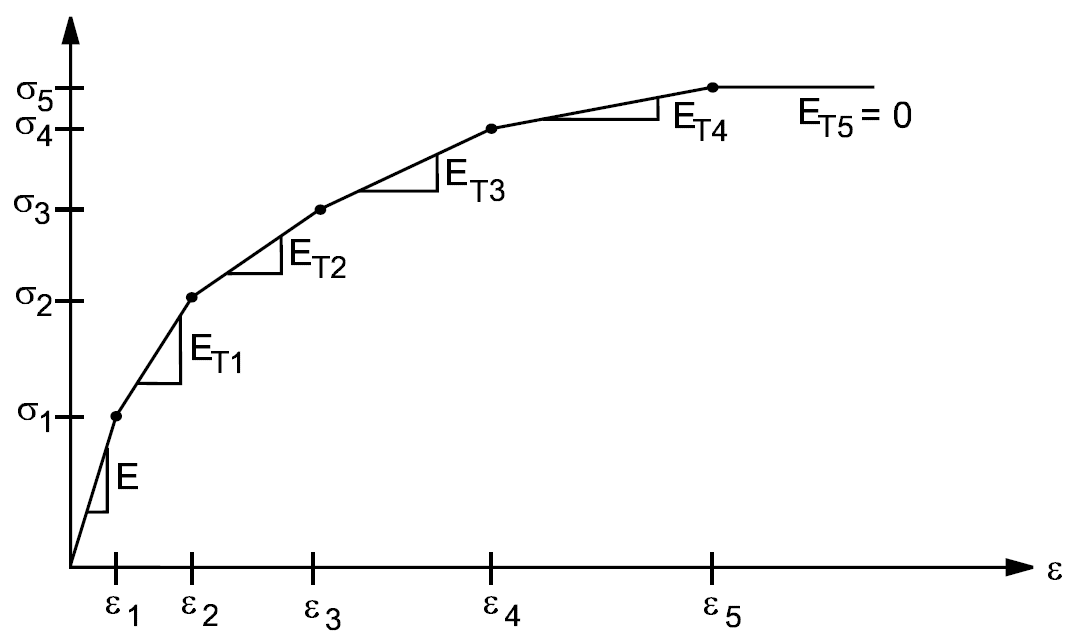
Рисунок 4.5 - Мультилинейная зависимость между деформациями и напряжениями

Весовые коэффициенты для каждого подъобъема с номером k определяются по формуле:

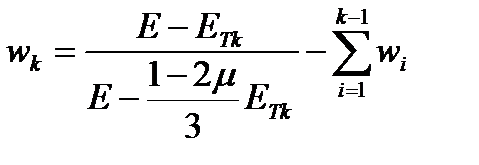. (4.32)

Предел текучести для каждого подъобъема, полагаемого идеально пластическим телом, вычисляется как:

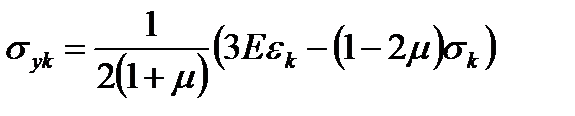, (4.33)

где ε _k, σ _k – ключевые точки на кривой напряжений-деформаций.

Число подъобъемов соответствует числу ключевых точек на кривой напряжений-деформаций

Приращение пластических деформаций {Δ ε ^pl_k } для каждого подъобъема определяется по критерию фон Мизеса и ассоциированного закона текучести.

Отдельно заметим, что раз каждый подъобъем принимается идеальным упруго-пластическим телом, то параметры { α _k } и C_k будут равны нулю.

Приращение пластических деформаций для полного объема получается следующим образом:

, (4.34)

где Nsw – количество подъобъемов.

Текущие пластические деформации и упругие деформации для полного объема вычисляются по известным уже соотношениям (4.16) и (4.17) соответственно:

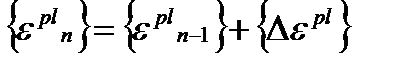и .

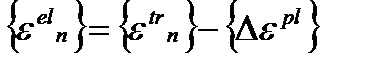Приращение эквивалентных пластических деформаций получается по формуле (4.23), а сами эквивалентные пластические деформации вычисляются также по известной (4.17) формуле:

.

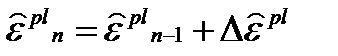Эквивалентные пластические напряжения определяются по кривой напряжений-деформаций (рисунок 4.5) по величине 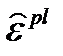по первому упругому компоненту кривой (аналогично тому, как показано на рисунке 4.4). Коэффициент напряжений N получается как отношение значений σ _e и σ _y для первого подъобъема.