
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение термина наибольшего и наименьшего значения функции
|
|
Наибольшим значением функции у=f(x) на промежутке X называют такое значение 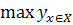 = f(
= f(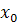 ), что для любого x
), что для любого x 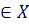 , x≠
, x≠ 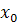 справедливо неравенство f(x)≤ f(
справедливо неравенство f(x)≤ f(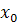 ).
).
Наименьшим значением функции y=f(x) на промежутке X называют такое значение 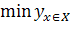 = f(
= f(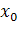 ),, что для любого x
),, что для любого x 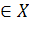 , x≠ t wx: val=" Cambria Math" /> < w: i/> < w: sz w: val=" 28" /> < w: sz-cs w: val=" 28" /> < /w: rPr> < m: t> x< /m: t> < /m: r> < /m: e> < m: sub> < m: r> < w: rPr> < w: rFonts w: ascii=" Cambria Math" w: fareast=" Times New Roman" w: h-ansi=" Cambria Math" /> < wx: font wx: val=" Cambria Math" /> < w: i/> < w: sz w: val=" 28" /> < w: sz-cs w: val=" 28" /> < /w: rPr> < m: t> 0< /m: t> < /m: r> < /m: sub> < /m: sSub> < /m: oMath> < /m: oMathPara> < /w: p> < w: sectPr wsp: rsidR=" 00000000" > < w: pgSz w: w=" 12240" w: h=" 15840" /> < w: pgMar w: top=" 1134" w: right=" 850" w: bottom=" 1134" w: left=" 1701" w: header=" 720" w: footer=" 720" w: gutter=" 0" /> < w: cols w: space=" 720" /> < /w: sectPr> < /w: body> < /w: wordDocument> ">
, x≠ t wx: val=" Cambria Math" /> < w: i/> < w: sz w: val=" 28" /> < w: sz-cs w: val=" 28" /> < /w: rPr> < m: t> x< /m: t> < /m: r> < /m: e> < m: sub> < m: r> < w: rPr> < w: rFonts w: ascii=" Cambria Math" w: fareast=" Times New Roman" w: h-ansi=" Cambria Math" /> < wx: font wx: val=" Cambria Math" /> < w: i/> < w: sz w: val=" 28" /> < w: sz-cs w: val=" 28" /> < /w: rPr> < m: t> 0< /m: t> < /m: r> < /m: sub> < /m: sSub> < /m: oMath> < /m: oMathPara> < /w: p> < w: sectPr wsp: rsidR=" 00000000" > < w: pgSz w: w=" 12240" w: h=" 15840" /> < w: pgMar w: top=" 1134" w: right=" 850" w: bottom=" 1134" w: left=" 1701" w: header=" 720" w: footer=" 720" w: gutter=" 0" /> < w: cols w: space=" 720" /> < /w: sectPr> < /w: body> < /w: wordDocument> "> 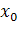 справедливо неравенство f(x)≥ f(t wx: val=" Cambria Math" /> < w: i/> < w: sz w: val=" 28" /> < w: sz-cs w: val=" 28" /> < /w: rPr> < m: t> x< /m: t> < /m: r> < /m: e> < m: sub> < m: r> < w: rPr> < w: rFonts w: ascii=" Cambria Math" w: fareast=" Times New Roman" w: h-ansi=" Cambria Math" /> < wx: font wx: val=" Cambria Math" /> < w: i/> < w: sz w: val=" 28" /> < w: sz-cs w: val=" 28" /> < /w: rPr> < m: t> 0< /m: t> < /m: r> < /m: sub> < /m: sSub> < /m: oMath> < /m: oMathPara> < /w: p> < w: sectPr wsp: rsidR=" 00000000" > < w: pgSz w: w=" 12240" w: h=" 15840" /> < w: pgMar w: top=" 1134" w: right=" 850" w: bottom=" 1134" w: left=" 1701" w: header=" 720" w: footer=" 720" w: gutter=" 0" /> < w: cols w: space=" 720" /> < /w: sectPr> < /w: body> < /w: wordDocument> ">
справедливо неравенство f(x)≥ f(t wx: val=" Cambria Math" /> < w: i/> < w: sz w: val=" 28" /> < w: sz-cs w: val=" 28" /> < /w: rPr> < m: t> x< /m: t> < /m: r> < /m: e> < m: sub> < m: r> < w: rPr> < w: rFonts w: ascii=" Cambria Math" w: fareast=" Times New Roman" w: h-ansi=" Cambria Math" /> < wx: font wx: val=" Cambria Math" /> < w: i/> < w: sz w: val=" 28" /> < w: sz-cs w: val=" 28" /> < /w: rPr> < m: t> 0< /m: t> < /m: r> < /m: sub> < /m: sSub> < /m: oMath> < /m: oMathPara> < /w: p> < w: sectPr wsp: rsidR=" 00000000" > < w: pgSz w: w=" 12240" w: h=" 15840" /> < w: pgMar w: top=" 1134" w: right=" 850" w: bottom=" 1134" w: left=" 1701" w: header=" 720" w: footer=" 720" w: gutter=" 0" /> < w: cols w: space=" 720" /> < /w: sectPr> < /w: body> < /w: wordDocument> "> 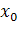 ).
).
Эти определения понятны: наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение на данном интервале при абсциссе t wx: val=" Cambria Math" /> < w: i/> < w: sz w: val=" 28" /> < w: sz-cs w: val=" 28" /> < /w: rPr> < m: t> x< /m: t> < /m: r> < /m: e> < m: sub> < m: r> < w: rPr> < w: rFonts w: ascii=" Cambria Math" w: fareast=" Times New Roman" w: h-ansi=" Cambria Math" /> < wx: font wx: val=" Cambria Math" /> < w: i/> < w: sz w: val=" 28" /> < w: sz-cs w: val=" 28" /> < /w: rPr> < m: t> 0< /m: t> < /m: r> < /m: sub> < /m: sSub> < /m: oMath> < /m: oMathPara> < /w: p> < w: sectPr wsp: rsidR=" 00000000" > < w: pgSz w: w=" 12240" w: h=" 15840" /> < w: pgMar w: top=" 1134" w: right=" 850" w: bottom=" 1134" w: left=" 1701" w: header=" 720" w: footer=" 720" w: gutter=" 0" /> < w: cols w: space=" 720" /> < /w: sectPr> < /w: body> < /w: wordDocument> "> 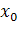 .
.
2.2 Алгоритм нахождения наибольшего и наименьшего значений функции f(x) на непрерывном отрезке 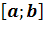 .
.
1) Найти производную 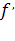 (x).
(x).
2) Найти стационарные и критические точки функции, лежащие на отрезке 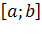
3) Вычислить значения функции y= f(x) в точках, отобранных на втором шаге, и в точках a и b: выбрать среди этих значений наименьшее и наибольшее.