Задача № 16. Найдите наибольшее значение площади прямоугольника со сторонами параллельными осям координат, и с диагональю OP

Найдите наибольшее значение площади прямоугольника со сторонами параллельными осям координат, и с диагональю OP, где О – начало координат, а Р – точка на графике функции .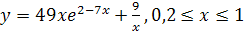

Решение:

Длины сторон прямоугольника равны положительным координатам точки Р. Поэтому его площадь равна их произведению: 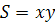. Исследуем функцию , 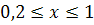с помощью производной.

.

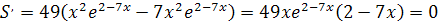Так как 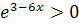, а по условию 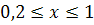, то 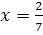– единственная критическая точка. Найдем значения функции S в концах отрезка [0, 2; 1] и сравним их с .

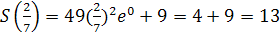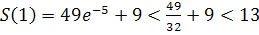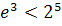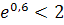Так как , то . Так как , то , , и .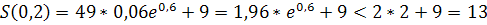

Ответ: 13.

Заключение

Над изучением этой темы работали многие ученые и философы. Много лет назад появились такие термины как функция, график, исследование функции и до сих пор они сохранились, приобретая новые черты и признаки.

Я выбрала эту тему, потому что мне было очень интересно узнать историю возникновения исследования функции. Мне кажется, что многим было бы интересно побольше узнать о функции, о ее свойствах и преобразованиях. Сделав эту курсовую работу, я систематизировала свои навыки пополнила свой запас знаний об этой теме.

Список используемой литературы

1. Мордкович А.Г. Алгебра и начала математического анализа 10-11кл. – Москва, 2009.

2. Мордкович А.Г. и др. Задачник по алгебре и началам математического анализа 10-11кл. – Москва, 2009.

3. Колмогоров А.Н., Абрамов А.М. и др. Алгебра и начала математического анализа 10-11кл. – Просвещение, 2008.

4. Башмаков М.И. Алгебра и начала анализа 10-11 кл. – Москва, 1992.

5. Мордкович А.Г., Семенов П.В. Алгебра и начала математического анализа 10-11кл. – Москва, 2010.

6. Виленкин Н.Я. Производная и задачи на экстремум // Квант, 1978 №6 с. 60-64.

7. Гусак А. А.. Высшая математика. Учебное пособие для студентов вузов в 2-х томах. – Мн., 1998. – 544 с. (1 т.), 448 с. (2 т.).

8. Кремер Н. Ш., Путко Б. А., Тришин И. М., Фридман М. Н. Высшая математика для экономистов: Учебник для вузов / Под ред. проф. Н. Ш. Кремера.– М.: ЮНИТИ, 2002. – 471 с.

9. Яблонский А. И., Кузнецов А. В., Шилкина Е. И. и др. Высшая математика. Общий курс: Учебник / Под общ. ред. С. А. Самаля.– Мн.: Выш. шк., 2000 г.

10. Ткачук В.В. Математика абитуриенту М: МЦНМО, 2008.