Задача №7

Найти наибольшее и наименьшее значения функции 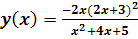на заданном отрезке .

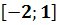Решение:

В этой задаче используется теорема о том, что непрерывная функция достигает своего наибольшего и наименьшего значений на отрезке: либо в критических точках, где производная обращается в нуль или не существует; либо на концах отрезка. Таким образом, для того, чтобы найти наибольшее и наименьшее значения функции на данном отрезке, необходимо найти её значения в критических точках и на концах отрезка, а затем сравнить эти значения.

Перепишем выражение функции в виде: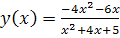

Найдем производную функции в виде: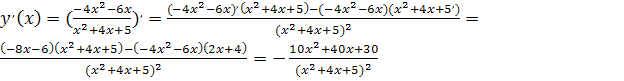

Найдем критические точки:

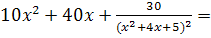. Отсюда 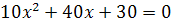10 или .

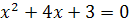Вычислим значения функции в найденной точке и на концах отрезка:

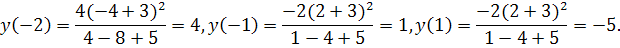
Сравнивая полученные значения, можем заключить, что наибольшее значение равно 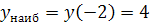, а наименьшее значение равно s New Roman" /> < wx: font wx: val=" Cambria Math" /> < w: i/> < w: sz w: val=" 28" /> < w: sz-cs w: val=" 28" /> < /w: rPr> < m: t> =-5< /m: t> < /m: r> < /m: oMath> < /m: oMathPara> < /w: p> < w: sectPr wsp: rsidR=" 00000000" > < w: pgSz w: w=" 12240" w: h=" 15840" /> < w: pgMar w: top=" 1134" w: right=" 850" w: bottom=" 1134" w: left=" 1701" w: header=" 720" w: footer=" 720" w: gutter=" 0" /> < w: cols w: space=" 720" /> < /w: sectPr> < /w: body> < /w: wordDocument> "> .

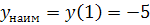Ответ: Наибольшее значение функции на отрезке равно .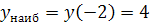

Наименьшее значение функции на отрезке равно 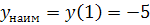.