Экстремум функции

Пусть 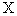- область определения функции 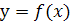и точка .

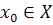Определение 1. Число М называется локальным максимумом функции 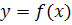, если существует такая окрестность точки 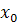, что для всех 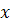из нее выполняется неравенство 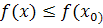. При этом М= 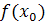, а сама точка 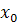называется точкой локального максимума.

Определение 2. Число m называется локальным минимумом функции 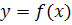, если существует такая окрестность точки 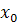, что для всех 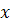из нее выполняется неравенство 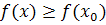. При этом m= 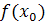, а сама точка 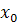называется точкой локального минимума.

Определение 3. Локальный максимум и локальный минимум называются локальными экстремумами. Соответствующая точка 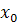называется точкой локального экстремума.

Теорема Ферма. Если функция 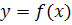имеет производную в точке 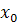и достигает в этой точке локального экстремума, то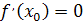

Определение 4. Точки, в которых производная функции равна нулю, называются стационарными точками.

Замечание. Функция может иметь экстремум и в точке, где эта функция не имеет производной. Например, 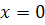- точка минимума функции , а 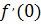не существует.

Определение 5. Точки, в которых функция имеет производную, равную нулю, или не является дифференцируемой, называют критическими точками.

Для того, чтобы точка 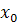была точкой экстремума функции 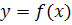, необходимо, чтобы 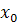являлась критической точкой данной функции.

Теорема 1. (достаточные условия того, что стационарная точка является точкой экстремума) Пусть функция 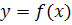дифференцируема на множестве 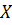, 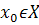- стационарная точка функци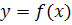и и 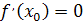. Тогда:

1) если при переходе через точку 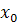производная функции 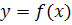меняет знак с “плюса” на “минус”, т. е. 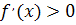слева от точк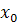и и 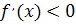справа от точки 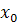, то - то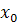чка локального максимума функции ;

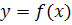2) если при переходе через точку 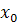производная функции 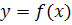меняет знак с “минуса” на “плюс”, то 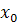- точка локального минимума функции .

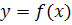Теорема 2. (достаточные условия того, что стационарная точка является точкой экстремума) Пусть функция 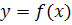дифференцируема на множестве 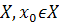, - стационарная точка функции 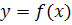и эта функция имеет вторую непрерывную производную в окрестности точки 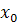. Тогда:

1) если 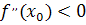, то - то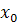чка локального максимума функции ;

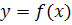2) если 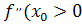, то 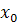- точка локального минимума функции .

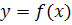Схема для решения задач на определение экстремума функций.

1. Установить область определения функции .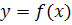

2. Найти её первую производную.

3. Найти стационарные точки функции 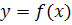, т.е. решить уравнение 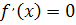, и точки, в которых 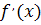не определена.

4. Определить знак производной на числовых интервалах, на которые стационарные и критические точки разбили область определения.