
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
II.Үй тапсырмасын тексеру
|
|
Ү й есебінің орындалуын тексеру жә не шығ ару жолын талдау.
ІII.Қ айталау, шолу сұ рақ тарына жауап алу.
- Пифагор теоремасы
- Герон формуласы
- косинустар теоремасы
- трапеция ауданының формуласы
- ү шбұ рыштар ұ қ састығ ы
ІII. Есептер шығ ару
№1. Есеп: Табандары 15 см, 5 см, ал бү йір қ абырғ асы 8 см жә не 6 см болатын трапецияның ауданын табың дар.
4 топқ а ә ртү рлі тә сілдер берілген жә не есептің шығ арылу жоспары кө рсетілген карточка беріледі.
№1 Пифагор теоремасы
| 1. ∆ АВH ү шбұ рышын қ арастырамыз. АВ=6 c, AH=x, BH-ны пифагор теоремасы арқ ылы ө рнектейміз. 2. СЕD тік бұ рышты ү шбұ рышын қ арасытрамыз. СD=8см, DE=(10-x)см Пифагор теоремасы арқ ылы СЕ-ны ө рнектейміз. 3. ВН=CE, x-ке қ атысты тең деу қ ұ рамыз. 4. Трапецияның біктігін табамыз. 5. Трапецияның ауданын табамыз. |
№2. Герон формуласы
| 1. СЕ│ │ АВ қ осымша сызық жү ргіземіз. 2. 2. АВСЕ – параллелограмм. 3. 3. СЕД ү шбұ рышын қ ұ растырамыз. Герон формуласы боцынша аудан табамыз. 4. 4. Ү шбұ рыштың табаны мен ауданы арқ ылы биіктігін табамыз. 5. Трапецияның ауданын табамыз. |
№3. Ү шбұ рыштар ұ қ састығ ы
| 1. АВ, СD қ абырғ аларының созындысын жү ргізіп, АВ∩ СD=E нү ктесін белгілейміз. 2. АЕD жә не ВЕС ү шбұ рыштарын қ ұ растырамыз. 3. Бұ л ү шбұ рыштар ұ қ састығ ымен ВЕ жә не ЕС табамыз. 4. Герон формуласымен АЕD ү шбұ рышының ауданын табамыз. 5. Герон формуласымен ВЕС ү шбұ рышының ауданын табамыз. 6. Трапеция ауданын табамыз |
. №4.
|
ІV. Тақ тада.
Ә р топ жетекшісі ө з тә сілімен тақ тада шығ ару керек, жә не тү сіндіруі қ ажет.
V. Ө з бетінше жұ мыс.
Есеп: Табандары 10 см, 24 см, ал бү йір қ абырғ алары 13 см жә не 15 см трапеция берілген. Трапецияның биіктігін жә не ауданын табың дар. (кез келген ә діспен шығ аруғ а болады.) Жұ мыстары тексерілініп бағ аланады.
VІ.Ү йге: АВСД трапециясының бү йір қ абырғ алары 8 см жә не 10 см, ВС табаны 2 см. АДС бұ рышының биссектрисасы АВ қ абырғ асының ортасы арқ ылы ө теді. Трапеция ауданын табың дар.
VII. Қ орытындылау.
Сабақ №__ 53 _
Кү ні: ______
Сынып: _ 11 ___
Сабақ тың тақ ырыбы: Жазық тық тар арасындағ ы бұ рыш. Екі жақ ты бұ рыш, оның сызық тық бұ рышы
Сабақ тың мақ саты:
Білімділік: Жазық тық тар арасындағ ы бұ рыш, екі жақ ты бұ рыш, оның сызық тық бұ рышы туралы білімдерін қ айталау
Дамытушылық: Ой қ орытындылау, логикалық ойлау қ абілетін дамытуғ а жетелеу.
Тә рбиелік: Ұ қ ыптылық пен байқ ағ ыштық қ а тә рбиелеу.
Сабақ тың тү рі: қ айталау сабақ
Сабақ тың барысы:
I.Ұ йымдастыру кезең і.
Оқ ушылардың сабақ қ а дайындығ ы жә не оқ у бө лмесінің, ақ параттық техниканың дайындығ ы тексеріледі. Оқ ушылармен сә лемдесу.
II. Қ айталау, шолу сұ рақ тарына жауап алу
1. Тү зу мен жазық тық арасындағ ы бұ рыш
2. Жазық тық тар арасындағ ы бұ рыштың анық тамасы
3. Екіжақ ты бұ рыш (бұ рыштың жағ ы, бұ рыштың қ ыры,) деген не?
4. Екіжақ ты бұ рыштың сызық тық бұ рышы деген не?
5. Екіжақ ты бұ рыштың ө лшеуіші сызық тық бұ рыштың қ алай таң дап алынғ андығ ына тә уелді болмайтындығ ы неліктен?
ІII. Есептер шығ ару
Тақ тада есептер шығ ару: №41, 42, 43
Ө здіктерінен есептер шығ ару: №44, 45
VII. Қ орытындылау.
Ү йге: №46, 47
Сабақ №__ 54 _
Кү ні: ______
Сынып: _ 11 ___
Сабақ тың тақ ырыбы: Жазық тық тар арасындағ ы бұ рыш. Екі жақ ты бұ рыш, оның сызық тық бұ рышы
Сабақ тың мақ саты:
Білімділік: Жазық тық тар арасындағ ы бұ рыш, екі жақ ты бұ рыш, оның сызық тық бұ рышы туралы білімдерін қ айталау
Дамытушылық: Ой қ орытындылау, логикалық ойлау қ абілетін дамытуғ а жетелеу.
Тә рбиелік: Ұ қ ыптылық пен байқ ағ ыштық қ а тә рбиелеу.
Сабақ тың тү рі: қ айталау сабақ
Сабақ тың барысы:
I.Ұ йымдастыру кезең і.
Оқ ушылардың сабақ қ а дайындығ ы жә не оқ у бө лмесінің, ақ параттық техниканың дайындығ ы тексеріледі. Оқ ушылармен сә лемдесу.
II. Қ айталау, шолу сұ рақ тарына жауап алу
a. Тү зу мен жазық тық арасындағ ы бұ рыш
b. Жазық тық тар арасындағ ы бұ рыштың анық тамасы
c. Екіжақ ты бұ рыш (бұ рыштың жағ ы, бұ рыштың қ ыры,) деген не?
d. Екіжақ ты бұ рыштың сызық тық бұ рышы деген не?
e. Екіжақ ты бұ рыштың ө лшеуіші сызық тық бұ рыштың қ алай таң дап алынғ андығ ына тә уелді болмайтындығ ы неліктен?
ІII. Есептер шығ ару
Тақ тада есептер шығ ару: №48, 49, 50
Ө здіктерінен есептер шығ ару: №51, 53
VII. Қ орытындылау.
Ү йге: №54, 55
№55
Сынып: 11 «б»
Кү ні: ___________
Сабақ тың тақ ырыбы: Векторларғ а амалдар қ олдану
Сабақ тың мақ саттары:
- Білімділік: Векторлардың координатасын табу, векторларды қ осу жә не азайту
2.Дамытушылық: Оқ ушылардың есеп шығ ару дағ дыларын дамыту.
3.Тә рбиелік: Оқ ушыларды дә лдікке, ұ қ ыптылық қ а, жылдамдылық қ а, ептілікке тә рбиелеу.
Сабақ тың тү рі: қ айталау сабағ ы
Сабақ тың ә дістері:
Сабақ тың кө рнекілігі:
Сабақ барысы: І Ұ йымдастыру кезең і:
а) Сә лемдесу ә) Оқ ушылар тізімін тексеру б) Сабақ тың мақ сатымен таныстыру.
ІІ Ө ткен тақ ырыпты қ айталау:
- Жазық тық тағ ы векторлар, вектордың координаталары
- Екі векторды ү шбұ рыш ережесі бойынша қ осу
- Екі векторды параллелограмм ережесі бойынша қ осу
- a жә не b векторларының айырымы деп b+х=a тең дігін қ анағ аттандыратын х векторын айтады
- Векторларды қ осудың қ асиеттері
ІІІ Дамыту кезең і. Есептер шығ ару:
1.A(2; 0; 0;), B(0; 0; 0), C(0; 2; 0), B1(0; 0; 2) ABCDA1B1C1D1 кубының тө белері болса, С1 нү ктесінің координаталарын табың ыз. Ж: C)(0; 2; 2)
2. M(2; 0; 0) H(0; 0; 0), P(0; 4; 0), H1(0; 0; 4) MHPKM1H1P1K1 тікбұ рышты параллелепипед тө белері болса, М1 нү ктесінің координатасын табың ыз. Ж: (2; 0; 4)
3.A(2; 0; 0), B(0; 0; 0), C(0; 2; 0), B1(0; 0; 2) ABCA1B1C1 призмасының тө белері 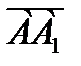 векторының координатасын табың ыз. Ж: (0; 0; 2)
векторының координатасын табың ыз. Ж: (0; 0; 2)
4. M(0; 0; 0), P(4; 4; 0), H(0; 4; 0), M1(0; 0; 6) МРНМ1Р1Н1 призманың тө белері. Р1 нү ктесінің координатасын табың ыз. Ж: (4; 4; 6)
5. 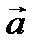 (1; 2; 3;) векторын
(1; 2; 3;) векторын  (1; 1; 0),
(1; 1; 0), 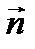 (1; 0; 1),
(1; 0; 1), 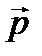 (0; 1; 1) векторлары арқ ылы жіктең із. Ж:
(0; 1; 1) векторлары арқ ылы жіктең із. Ж: 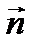 +2
+2 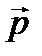
6. ABCD параллелограмм болса, 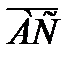 +
+ 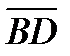 –2
–2 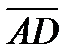 векторларының қ осындысын анық таң ыз. Ж: 0
векторларының қ осындысын анық таң ыз. Ж: 0
7. M(2; 0; 0) H(0; 0; 0), P(0; 4; 0), H1(0; 0; 4) MHPKM1H1P1K1 тікбұ рышты параллелепипед тө белері болса, 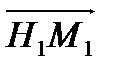 векторынынң координатасын табың ыз. Ж. (2; 0; 0)
векторынынң координатасын табың ыз. Ж. (2; 0; 0)
Сабақ ты бекіту кезең і:
- Векторларды қ осу жә не азайту
Сабақ ты қ орытындылау: Оқ ушыларғ а сабақ қ а қ атысқ анына сай бағ а қ ою.
Ү й жұ мысы:
1.M(0; 0; 0), P(4; 4; 0), H(0; 4; 0), M1(0; 0; 6) МРНМ1Р1Н1 призманың тө белері. Р1 нү ктесінің координатасын табың ыз. Ж. (4; 4; 6)
2. M(0; 0; 0), P(4; 4; 0), H(0; 4; 0), M1(0; 0; 6) МРНМ1Р1Н1 призманың тө белері. 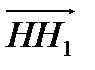 векторының координатасын табың ыз. Ж. (0; 0; 6)
векторының координатасын табың ыз. Ж. (0; 0; 6)
№56
Сынып: 11 «б»
Кү ні: ___________
Сабақ тың тақ ырыбы: Векторларғ а амалдар қ олдану
Сабақ тың мақ саттары:
- Білімділік: Векторлардың скалыр кө бейтіндісі
2.Дамытушылық: Оқ ушылардың есеп шығ ару дағ дыларын дамыту.
3.Тә рбиелік: Оқ ушыларды дә лдікке, ұ қ ыптылық қ а, жылдамдылық қ а, ептілікке тә рбиелеу.
Сабақ тың тү рі: қ айталау сабағ ы
Сабақ тың ә дістері:
Сабақ тың кө рнекілігі:
Сабақ барысы: І Ұ йымдастыру кезең і:
а) Сә лемдесу ә) Оқ ушылар тізімін тексеру б) Сабақ тың мақ сатымен таныстыру.
ІІ Ө ткен тақ ырыпты қ айталау:
1) Векторлардың скаляр кө бейтіндісі олардың абсолют шамаларын олардың арасындағ ы бұ рыштың косинусына кө бейткенге тең. a´ b=/a/´ /b/cos(ab)
2) Координаталық i, j векторларының скалярлық кө бейтіндісі:
i´ i =/ i /´ / i /cos00=/ i/2=1
j ´ j =/ j /´ /j /cos00=/ j /2=1
i´ j =/ i /´ / j /cos900=0
3) Теорема: Екі вектордың скалярлық кө бейтіндісі олардың сә йкес координаталарының кө бейтінділерінің қ осындысына тең. a´ b= a1 b1 +a2 b2
ІІІ Дамыту кезең і. Есептер шығ ару:
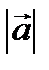 =2,
=2, 
 =3, арасындағ ы бұ рышы 1200 болса, (2
=3, арасындағ ы бұ рышы 1200 болса, (2 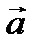 +3
+3 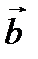 )(
)(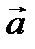 –
–  ) скаляр кө бейтіндісін табың ыз.
) скаляр кө бейтіндісін табың ыз.
Ж: -22
2. A(1; 2), B(2; 3), C(-1; 4), D(3; -2) болса, (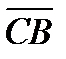 +
+ 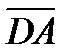 )(
)(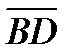 –
– 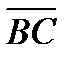 ) скаляр кө бейтіндісін табың ыз.
) скаляр кө бейтіндісін табың ыз.
Ж. -14
3. A(1; 2), B(2; 3), C(-1; 4), D(3; -2) болса, 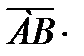
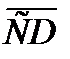 скаляр кө бейтіндісін табың ыз
скаляр кө бейтіндісін табың ыз
Ж. -2
4. A(1; 2), B(2; 3), C(-1; 4), D(3; -2) болса, 
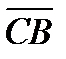 скаляр кө бейтіндісін табың ыз.
скаляр кө бейтіндісін табың ыз.
Ж. 2
5. А(3; - 1; 1), В(1; - 1; 3), С(3; 1; - 1) ү шбұ рыштың тө белері болса, 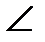 АВС бұ рышын табың ыз.
АВС бұ рышын табың ыз.
Ж. 300
6: А(-1; -2; 4), В(-4; -2; 0), С(3; -2; 1) ү шбұ рышының тө белері болса, А тө бесіндегі ү шбұ рыштың бұ рышын табың ыз. Ж. 900
7. А(14; -8; -1), В(7; 3; -1), C(-6; 4; -1) АВСD ромбысының тө белері болса, ромбтың сү йір бұ рышын табың ыз. Ж. arccos 3/5
Сабақ ты бекіту кезең і:
- Векторларды қ осу жә не азайту
- Векторлардың скалыр кө бейтіндісі
Сабақ ты қ орытындылау: Оқ ушыларғ а сабақ қ а қ атысқ анына сай бағ а қ ою.
Ү й жұ мысы:
1. DАВС дұ рыс тетраэдр қ ыры 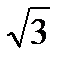 . М нү ктесі АС кесіндісінің ортасы.
. М нү ктесі АС кесіндісінің ортасы.  жә не
жә не 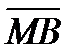 векторлардың скаляр кө бейтіндісі. Ж. -1, 5
векторлардың скаляр кө бейтіндісі. Ж. -1, 5
2. 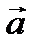 =3
=3  +2
+2 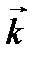 жә не
жә не 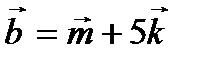 векторлар арасындағ ы бұ рышты табың ыз, мұ ндағ ы
векторлар арасындағ ы бұ рышты табың ыз, мұ ндағ ы
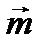 жә не
жә не 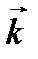 бірлік векторлар. Ж. 450
бірлік векторлар. Ж. 450
№57
Сынып: 11 «б»
Кү ні: ___________
Сабақ тың тақ ырыбы: Векторлар тақ ырыбына есептер
Сабақ тың мақ саттары:
- Білімділік: Векторлардың тақ ырыбына есептер шығ ару дағ дыларын дамыту
2.Дамытушылық: Оқ ушылардың есеп шығ ару дағ дыларын дамыту.
3.Тә рбиелік: Оқ ушыларды дә лдікке, ұ қ ыптылық қ а, жылдамдылық қ а, ептілікке тә рбиелеу.
Сабақ тың тү рі: қ айталау сабағ ы
Сабақ тың ә дістері:
Сабақ тың кө рнекілігі:
Сабақ барысы: І Ұ йымдастыру кезең і:
а) Сә лемдесу ә) Оқ ушылар тізімін тексеру б) Сабақ тың мақ сатымен таныстыру.
ІІ Дамыту кезең і. Есептер шығ ару:
1. 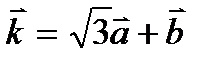 жә не
жә не 
 векторлар арасындағ ы бұ рышты табың ыз, мұ ндағ ы
векторлар арасындағ ы бұ рышты табың ыз, мұ ндағ ы 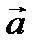 жә не
жә не 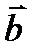 бірлік векторлар. Ж: 300
бірлік векторлар. Ж: 300
2. HPMKE пирамидасының қ ырлары тең (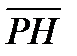 –
– 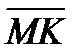 )(
)(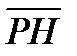 +
+ 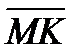 )+
)+ 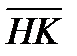 (
(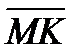 +
+ 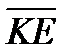 ) векторлық ө рнегін ық шамда. Ж. 0
) векторлық ө рнегін ық шамда. Ж. 0
3. 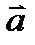 жә не
жә не 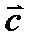 векторлар арасындағ ы бұ рыш
векторлар арасындағ ы бұ рыш 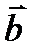 жә не
жә не 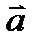 векторлары арасындағ ы бұ рышқ а тең жә не олар 600-қ а тең,
векторлары арасындағ ы бұ рышқ а тең жә не олар 600-қ а тең, 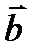 жә не
жә не 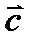 перпендикуляр.
перпендикуляр. 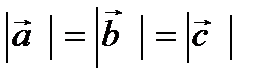 =x болса,
=x болса, 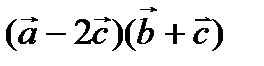 скаляр кө бейтіндісін есептең із. Ж. -x2
скаляр кө бейтіндісін есептең із. Ж. -x2
4.BACD тетраэдр 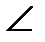 BDC=
BDC= 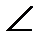 BDA=
BDA= 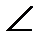 DCA=900,
DCA=900, 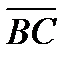 =3,
=3, 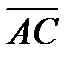 =4.
=4. 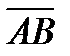
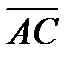 +
+ 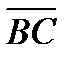
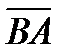 +
+ 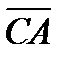
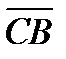 векторлық қ осындысын анық таң ыз. Ж: 25
векторлық қ осындысын анық таң ыз. Ж: 25
5. 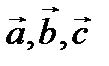 векторлары ө зара перпендикуляр.
векторлары ө зара перпендикуляр. 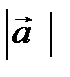 =y болса,
=y болса, 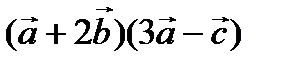 скаляр кө бейтіндісін анық таң ыз. Ж: 3y2
скаляр кө бейтіндісін анық таң ыз. Ж: 3y2
6. PHKM пирамида РМ қ ыры биіктік, РКН=900. МК=6, KH=8 болса 
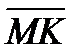 +
+ 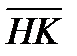
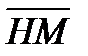 +
+ 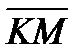
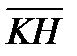 қ осындысын табың ыз. Ж: 100
қ осындысын табың ыз. Ж: 100
7. 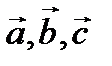 векторлары келесі шарттарды қ анағ аттандырады
векторлары келесі шарттарды қ анағ аттандырады 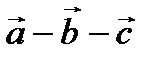 =0,
=0, 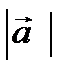 =3,
=3,
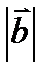 =4,
=4,  =5. Есепте.
=5. Есепте. 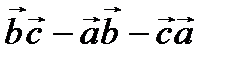 . Ж: -25
. Ж: -25
Сабақ ты бекіту кезең і:
- Векторлардың скаляр кө бейтіндісі
- Векторларды қ осу жә не азайту
Сабақ ты қ орытындылау: Оқ ушыларғ а сабақ қ а қ атысқ анына сай бағ а қ ою.
Ү й жұ мысы:
1. 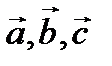 векторлары келесі шарттарды қ анағ аттандырады
векторлары келесі шарттарды қ анағ аттандырады 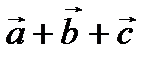 =0
=0 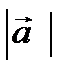 =1,
=1,
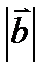 =4,
=4,  =5. Есептең із:
=5. Есептең із: 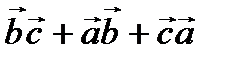 . Ж. -21
. Ж. -21
2. A(10; 0; 0) нү ктесінен B(0; 0; 0), C(8; 6; 0;) нү ктелерін басып ө тетін тү зуге дейінгі қ ашық тық ты табың ыз. Ж: 6
№58
Сынып: 11 «б»
Кү ні: ___________
Сабақ тың тақ ырыбы: Векторлар тақ ырыбына есептер
Сабақ тың мақ саттары:
- Білімділік: Векторлар тақ ырыбына есептер шығ ару дағ дыларын дамыту
2.Дамытушылық: Оқ ушылардың есеп шығ ару дағ дыларын дамыту.
3.Тә рбиелік: Оқ ушыларды дә лдікке, ұ қ ыптылық қ а, жылдамдылық қ а, ептілікке тә рбиелеу.
Сабақ тың тү рі: қ айталау сабағ ы
Сабақ тың ә дістері:
Сабақ тың кө рнекілігі:
Сабақ барысы:
І Ұ йымдастыру кезең і:
а) Сә лемдесу ә) Оқ ушылар тізімін тексеру б) Сабақ тың мақ сатымен таныстыру.
ІІ Дамыту кезең і. Есептер шығ ару:
1.АВСDА1В1С1D1 куб қ ырының ұ зындығ ы 2. АВ1 жә не СС1 векторларының скаляр кө бейтіндісін табың ыз. Ж: 4
2. А(3; - 1; 1), В(1; - 1; 3), С(3; 1; - 1) ү шбұ рыштың тө белері болса, 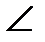 АВС бұ рышын табың ыз.
АВС бұ рышын табың ыз.
Ж: 300
3. ЕАВСD дұ рыс пирамида қ ыры 2-ге тең, О – табан диагональдарының қ иылысу нү ктесі. ВЕ жә не CD векторларының скаляр кө бейтіндісін табың ыз. Ж.2
4. А(-1; -2; 4), В(-4; -2; 0), С(3; -2; 1) ү шбұ рышының тө белері болса, А тө бесіндегі ү шбұ рыштың бұ рышын табың ыз. Ж: 900
5. DАВС дұ рыс тетраэдр. 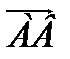 жә не
жә не 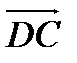 векторларының скаляр кө бейтіндісін табың ыз.
векторларының скаляр кө бейтіндісін табың ыз.
Ж: 0
6.DАВС дұ рыс тетраэдр қ ыры 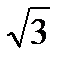 . М нү ктесі АС кесіндісінің ортасы.
. М нү ктесі АС кесіндісінің ортасы.  жә не
жә не 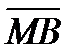 векторлардың скаляр кө бейтіндісі. Ж: -1, 5
векторлардың скаляр кө бейтіндісі. Ж: -1, 5
7. 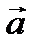 =3
=3  +2
+2 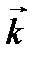 жә не
жә не 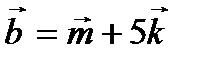 векторлар арасындағ ы бұ рышты табың ыз, мұ ндағ ы
векторлар арасындағ ы бұ рышты табың ыз, мұ ндағ ы
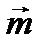 жә не
жә не 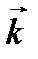 бірлік векторлар. Ж: 450
бірлік векторлар. Ж: 450
Сабақ ты бекіту кезең і:
- Векторлардың скаляр кө бейтіндісі
- Векторларды қ осу жә не азайту
Сабақ ты қ орытындылау: Оқ ушыларғ а сабақ қ а қ атысқ анына сай бағ а қ ою.
Ү й жұ мысы:
1. АВСD дұ рыс тетраэдр. 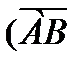 +
+ 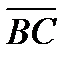 )(
)(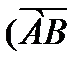 –
– 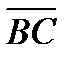 )+
)+ 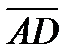 (
(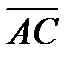 –
– 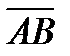 ) векторлық ө рнекті ық шамдаң ыз.
) векторлық ө рнекті ық шамдаң ыз.
Сабақ №__ 59 __
Кү ні: ______
Сынып: _ 11 ___
Тақ ырыбы: Есептер шығ ару
Мақ саты:
1. Векторларғ а амалдар қ олдану тақ ырыбына есептер шығ ару дағ дыларын дамыту.
2.Кең істікті елестету арқ ылы бейнелеу дағ дыларын, талдау жасай білу, жалпылау, жү йелеу жә не қ орытынды жасай алу біліктерін дамытуғ а жағ дай жасау.
3.Оқ ушыларды белсенді танымдық іс-ә рекетке жұ мылдыру арқ ылы пә нге деген ынтасын, қ ызығ ушылығ ын арттыруғ а, кә сіби бағ дар беруге мү мкіндік туғ ызу.
Типі: Практикалық сабақ.
Сабақ тың кө рнекілігі: тү рлі сызбалар
Сабақ тың барысы:
1.Ұ йымдастыру кезең і.
Оқ ушылардың сабақ қ а дайындығ ы жә не оқ у бө лмесінің, ақ параттық техниканың дайындығ ы тексеріледі. Оқ ушылармен сә лемдесу.
2.Есептер шығ ару
1.А(14; -8; -1), В(7; 3; -1), C(-6; 4; -1) АВСD ромбысының тө белері болса, ромбтың сү йір бұ рышын табың ыз. Ж: arccos 3/5
2. АВСD дұ рыс тетраэдр. 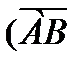 +
+ 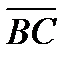 )(
)(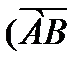 –
– 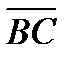 )+
)+ 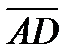 (
(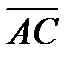 –
– 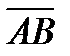 ) векторлық ө рнекті ық шамдаң ыз.
) векторлық ө рнекті ық шамдаң ыз.
Ж: 0
3.HPMKE пирамидасының қ ырлары тең (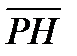 –
– 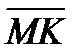 )(
)(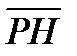 +
+ 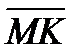 )+
)+ 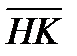 (
(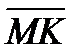 +
+ 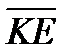 ) векторлық ө рнегін ық шамда. Ж: 0
) векторлық ө рнегін ық шамда. Ж: 0
4. 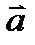 жә не
жә не 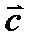 векторлар арасындағ ы бұ рыш
векторлар арасындағ ы бұ рыш 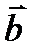 жә не
жә не 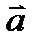 векторлары арасындағ ы бұ рышқ а тең жә не олар 600-қ а тең,
векторлары арасындағ ы бұ рышқ а тең жә не олар 600-қ а тең, 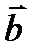 жә не
жә не 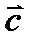 перпендикуляр.
перпендикуляр. 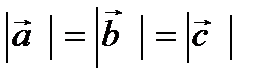 =x болса,
=x болса, 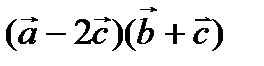 скаляр кө бейтіндісін есептең із. Ж: -x2
скаляр кө бейтіндісін есептең із. Ж: -x2
5.BACD тетраэдр 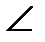 BDC=
BDC= 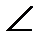 BDA=
BDA= 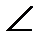 DCA=900,
DCA=900, 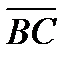 =3,
=3, 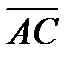 =4.
=4. 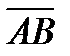
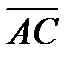 +
+ 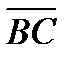
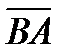 +
+ 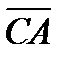
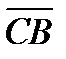 векторлық қ осындысын анық таң ыз. Ж: 25
векторлық қ осындысын анық таң ыз. Ж: 25
6. 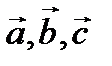 векторлары келесі шарттарды қ анағ аттандырады
векторлары келесі шарттарды қ анағ аттандырады 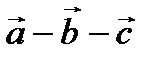 =0,
=0, 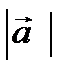 =3,
=3, 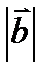 =4,
=4,  =5. Есепте.
=5. Есепте. 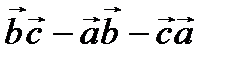 . Ж. -25
. Ж. -25
7. 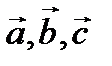 векторлары келесі шарттарды қ анағ аттандырады
векторлары келесі шарттарды қ анағ аттандырады 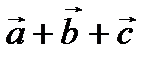 =0
=0 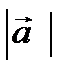 =1,
=1, 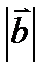 =4,
=4,  =5. Есептең із:
=5. Есептең із: 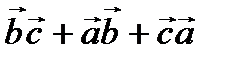 . Ж. -21
. Ж. -21
Ү й жұ мысы:
A(10; 0; 0) нү ктесінен B(0; 0; 0), C(8; 6; 0;) нү ктелерін басып ө тетін тү зуге дейінгі қ ашық тық ты табың ыз. Ж. 6
Оқ ушыларғ а сабақ қ а қ атысқ анына сай бағ а қ ою
№
Пә н: геометрия
Сынып: 11 «б»
Кү ні: __________
Сабақ тың тақ ырыбы: Шең бер жә не оның элементтерінің қ асиеттері. Шең бер мен тү зудің ө зара орналасуы. Дө ң гелек
Сабақ тың мақ саты:
білімділік: Шең бер, дө ң гелек жә не оның элементтерінің анық тамасын білу. Шең бер мен тү зудің ө зара орналасу жағ дайларын білу. Хордағ а перпендикуляр диаметр туралы теореманы дә лелдемесін қ айталау.
тә рбиелік: Оқ ушыларды адамгершілікке, ұ йымшылдық қ а, бірлікке, ұ қ ыптылық қ а, ө з бетімен білім алуғ а тә рбиелеу
дамытушылық: Оқ ушылардың пә нге деген қ ызығ ушылығ ын арттыру жә не ойлау, есте сақ тау қ абілеттерін, математикалық тіл байлығ ын дамыту.
Сабақ тың типі: Қ айталау
Сабақ тың кө рнекілігі: Интербелсенді тақ та
Сабақ тың ә дісі: сұ рақ -жауап, ақ параттық, практикалық
Сабақ тың жү рісі:
І.Ұ йымдастыру. Сабақ мақ сатымен таныстыру
ІІ. Қ айталау
1) Шең бер элементтері: центр, радиус, диаметр, хорда, доғ а, жанама
2) Шең бер мен тү зудің орналасуы 1) һ > r, 2) h < r 3) h = r
3) Шең бердің ұ зындығ ының формуласы
4) Дө ң гелек элементтері: центр, радиус, сектор, сегмент
5) Дө ң гелектің ауданы, сектордың ауданы
ІІІ.Есептер шығ ару
1. Шең бердің АД жә не ВС хордалары қ иылысады. Егер 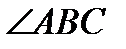 бұ рышы 600, ал
бұ рышы 600, ал 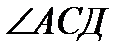 бұ рышы 700 тең болса, онда
бұ рышы 700 тең болса, онда 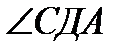 бұ рышын табың ыз. Жауабы: 600
бұ рышын табың ыз. Жауабы: 600
2. Тік бұ рышты ү шбұ рыштың гипотенузасы 10 см-ге тең. Осы ү шбұ рышқ а сырттай сызылғ ан шең бердің радиусын табың ыз. Жауабы: 5см
3.Ү шбұ рыштың қ абырғ асы 10 см, ал оғ ан қ арсы жатқ ан бұ рыш 1500. Осы ү шбұ рышқ а сырттай сызылғ ан шең бердің радиусын табың ыз. Жауабы: 10 см
4. Тік бұ рышты ү шбұ рыштың катеттері 6 жә не 8. Осы ү шбұ рышқ а іштей жә не сырттай сызылғ ан шең берлердің радиустарының қ осындысын табың ыз: Жауабы: 7
5. Бө ренеден кө лденең қ имасының ауданы 9 см2 болатын дұ рыс тө ртбұ рышты тақ тай кесіліп алынғ ан. Бө рененің диаметрін табың ыз. Жауабы: 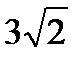
6. Тік тө ртбұ рышты ү шбұ рыштың катеттері 30 см жә не 40 см. Оғ ан сырттай сызылғ ан шең бердің радиусын табың ыз: Жауабы: 25 см
VІІ. Бағ алау
VІІІ. Ү йге тапсырма:
№1. Шең бердің радиусы 2, 5 см-ге тең. Шең бер хордасы 6 см- ге тең болуы мү мкін бе? (Д = 5 см, хорда 6 см болуы мү мкін емес)
№2. Ө зара перпендикуляр хордалар бір-бірін 5 см жә не 7 см кесінділерге бө леді. О нү ктесінен хордағ а тү сірілген перпендикулярды табың дар.
№3. АВ жә не СД центрі О болатын шең бердің диаметрі. Егер СВ = 13 см, АВ = 16 см болса, АОД ү шбұ рышының периметрі неге тең болады?
№61
Кү ні:
Сабақ тың тақ ырыбы: Ү шбұ рыштар. Қ айталау.
Сабақ тың мақ саты:
Білімділік: Ү шбұ рыштардың қ асиеттерін қ олданып есептер шығ ару
Дамытушық: есте сақ тау, зейін қ ою, ө зіндік ойлау қ абілеттерін дамыту
Тә рбиешілік: жауапкершілік, белсенділік, білімге талпыну қ асиеттерін бойында терең дету
Сабақ тың тү рі: Қ айталау, іздену сабағ ы
Сабақ тың барысы:
1.Ұ йымдастыру кезең і: тү гендеу, сабақ қ а ынталандыру
2.Қ айталау сұ рақ тары:
1. Ү шбұ рыштардың тү рлері
2. Элементтері
3. Биссектриса, медиана, биіктік. Анық тама беру
4. Бұ рыштардың тү рлері (сү йір, доғ ал, тік, вертикаль, сыбайлас, ішкі, сыртқ ы...)
5. Ү шбұ рыштың бұ рыштарының қ осындысы
6. Ү шбұ рыш тең сіздігі
7. Ү шбұ рыштың тең дігінің белгілері
3. Есептер шығ ару кезең і
1. Ү шбұ рыштың бү йір қ абырғ алары 30 см жә не 25 см, ал табаны 11 см-ге тең. ү шбұ рыштың табанына жү ргізілген биіктігін табың ыз. Жауабы: 24 см
2. Тең бү йірлі ү шбұ рыштың бү йір қ абырғ асы 17 см, ал табаны 16 см. Табанына тү сірілген биіктігін табың ыз. Жауабы: 15 см
3. Қ абырғ алары a жә не b болатын АВС ү шбұ рышы берілген жә не осы қ абырғ алр арасындағ ы бұ рышы с болатын. С тө бесінен шығ атын биссектрисаның ұ зындығ ы неге тең?
Жауабы: 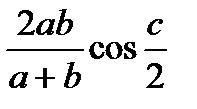
4. Тік бұ рышты ү шбұ рыштың катеттерінің ұ зындық тары сә йкес 12 жә не 5-ке тең. Тік бұ рыштан шығ атын биссектриса гипотенузаны ұ зындық тары қ андай кесінділерге бө леді?
Жауабы: 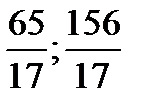
5. Тік бұ рышты ү шбұ рыштың катеттерінің ұ зындық тары сә йкес  жә не
жә не 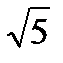 -ке тең. Тік бұ рыштан шығ атын биссектриса гипотенузаны ұ зындық тары қ андай кесінділерге бө леді?
-ке тең. Тік бұ рыштан шығ атын биссектриса гипотенузаны ұ зындық тары қ андай кесінділерге бө леді?
Жауабы: 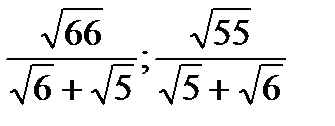
6. Тік бұ рышты ү шбұ рыштың катеттерінің ұ зындық тары 3 жә не 4-ке тең. Тік бұ рыштан шығ атын биссектриса гипотенузаны ұ зындық тары қ андай кесінділерге бө леді?
Жауабы: 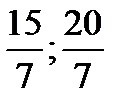
7. АВС ү шбұ рышының СВ, СА жә не АВ қ абырғ алары сә йкес 4 см, 3 см, 2 см болатын болса, онда биссектрисалардың қ иылысу нү ктесі В бұ рышының биссектрисасын қ андай қ атынаста бө леді? (В тө бесінен бастап есептегенде).
Жауабы: 2: 1
Қ орытындылау, бағ алау
Ү йге тапсырма беру: Тө ртбұ рыштар
1. Егер тік бұ рышты ү шбұ рыштың тік бұ рышынан гипотенузағ а тү сірілген биіктік оны 3 см, 27 см бө ліктерге бө летін болса, онда осы биіктіктің ұ зындығ ы қ андай? Жауабы: 9 см
2. ДО кесіндісі ДВС ү шбұ рышының биссектрисасы. Егер ВО=8 см, ВС=22 см6 ВД=12 см болса, ДС-ны табың ыз. Жауабы: 21 см
№62
Пә н: геометрия
Сынып: 11 «б»
Кү ні: __________
Сабақ тың тақ ырыбы: Тө ртбұ рыштар.
Сабақ тың мақ саттары:
1. Білімділік: Тө ртбұ рыштар жә не олардың тү рлері мен қ асиеттері.
2. Дамытушылық: Тө ртбұ рыштардың ортақ қ асиеттері.
3. Тә рбиелік: Оқ ушылардың еске тү сіру қ абілеттерін дамыту.
Сабақ тың тү рі: қ айталау сабағ ы
Сабақ тың ә дістері:
Сабақ тың кө рнекілігі:
Сабақ барысы: І Ұ йымдастыру кезең і:
а) Сә лемдесу ә) Оқ ушылар тізімін тексеру б) Сабақ тың мақ сатын нұ сқ ау
ІІ Ө ткен тақ ырыпты қ айталау:
-Параллелограмм
-Тіктө ртбұ рыш, ромб, квадрат
-Трапеция
ІІІ Есептер шығ ару:
1. АВСD тіктө ртбұ рышындағ ы А бұ рышының биссектрисасы СD қ абырғ асын СК=15, 3см жә не DK=18, 4см кесінділерге бө леді. АВСD тіктө ртбұ рышының периметрін жә не АВСК трапециясының орта сызығ ының ұ зындығ ын табың дар.
2. Параллелограмның бір қ абырғ асы екіншісінен 12см ұ зын. Егер оның периметрі 220см болса, параллелограмның қ абырғ алары неге тең?
3. Трапецияның орта сызығ ының ұ зындығ ы 24см-ге тең. Табандарының қ атынасы 5: 3. трапецияның табандарының ұ зындығ ын табындар.
4. АВСD Параллелограмында ВАD бұ рышының АN биссектрисасы ВС қ абырғ асын ВN=11см жә не NC=5см кесінділерге бө леді. Параллелограмның периметрін жә не ANCD трапециясының орта сызығ ының ұ зындығ ын табындар.
5. Тіктө ртбұ рыштың диагоналі 28см, ал кіші қ абырғ асы 14см. Диагональдарының арасындағ ы бұ рышты табындар.
6. Трапецияның табандарының айырмасы 6см, ал оның орта сызығ ының ұ зындығ ы 10см. Трапецияның табандарының ұ зындығ ын табындар.
Сабақ ты қ орытындылау: Оқ ушыларғ а сабақ қ а қ атысқ анына сай бағ а қ ою.
Ү й жұ мысы:
1. Бір қ абырғ асы 72 см жә не ол периметрінің 3: 8 бө лігіне тең болатын параллелограмның қ абырғ аларын табың дар. Жауабы: 24 см жә не 72 см
2. Периметрі 44 см-ге тең болатын параллелограмм диоганімен ә рқ айсысының периметрі 30 см болатын екі ү шбұ рышқ а бө лінген. Диагональдің ұ зындығ ын табың ыз. Жауабы: 8 см
Сабақ №__
Кү ні: ______
Сынып: _ 11___
Сабақ тың тақ ырыбы: Дұ рыс кө пбұ рыштар.
Сабақ тың мақ саты:
Білімділік. Дұ рыс кө пбұ рыштар анық тамасын жә не қ асиеттерін қ айталау, есептер шығ ару дағ дыларын дамыту.
Дамытушылық: Кең істікті елестету арқ ылы бейнелеу дағ дыларын, талдау жасай білу, жалпылау, жү йелеу жә не қ орытынды жасай алу біліктерін дамытуғ а жағ дай жасау..
Тә рбиелік: Оқ ушыларды дә лдікке тә рбиелеу. Оқ ушылардың теориялық білімін тә жірибеде қ олдануда ө з-ө зіне сенімділігін арттыру
Сабақ тың типі: Қ айталау сабағ ы.
Сабақ тың тү рі: Практикалық сабақ.
Сабақ тың кө рнекілігі: Интерактивті тақ та, слайдтар
Сабақ тың жоспары:
1. Ұ йымдастыру кезең і. Оқ ушылардың сабақ қ а даярлығ ын, қ ұ рал – жабдық тарының болуын қ адағ алау жә не топтарғ а бө ліп отырғ ызу.
2. Ү й тапсырмасын тексеру. Оқ ушының жан – жақ ты білімін тексеру: