Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кеңістіктегі түзудің жалпы теңдеуі
|
|
Тү зуді екі жазық тық тың тың қ иылысу арқ ылы былай анық талады: 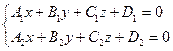 . Бұ лардың нормаль ваекторларының координаталары былайша анық талады:
. Бұ лардың нормаль ваекторларының координаталары былайша анық талады: 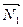 (A1, B1, C1),
(A1, B1, C1), 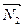 (A2, B2, C2);
(A2, B2, C2);
Тү зудің бағ ыттауыш векторы 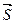
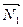 ,
, 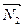 векторларына перпендикуляр. Сонда
векторларына перпендикуляр. Сонда 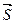 =
= 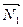 x
x 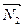 Þ
Þ 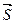
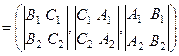 .
.
Жазық тық векторлық формада тө мендегі тең деу арқ ылы берілуі мү мкін:
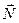 ×
× 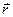 + D = 0, где
+ D = 0, где
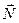 - жазық тық тың нормалі;
- жазық тық тың нормалі; 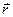 -Жазық тық тың кез келген нү ктесінің радиус - векторы.
-Жазық тық тың кез келген нү ктесінің радиус - векторы.
Айталық кең істікте екі жазық тық берілсін: 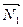 ×
× 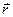 + D1 = 0 и
+ D1 = 0 и 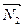 ×
× 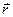 + D2 = 0, нормаль векторлардың координаталары::
+ D2 = 0, нормаль векторлардың координаталары:: 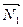 (A1, B1, C1),
(A1, B1, C1), 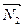 (A2, B2, C2);
(A2, B2, C2); 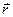 (x, y, z).
(x, y, z).
Тү зудің жалпы тең деуі параметрлік тү рде беріледі:

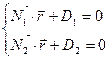
Тү зудің координаталық формадағ ы жалпы тең деуі:

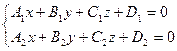
Бұ л практика жү зінде есеп тең деуі жалпы тү рде берілген тү зулердің тең деулерін канондық тү рге келтіру болып табылады.
Ол ү шін тү зудің кез келген нү ктесін жә не m, n, p сандарын табады.
Бұ л ұ шін тү зудің бағ ыттаушы векторы берілген жазық тық тардың нормаль векторлардың векторлық кө бейтіндісі арқ ылы анық талады.
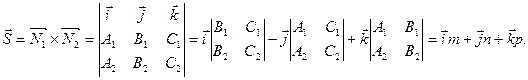
Мысалы. Тү зудің 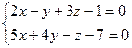 канондық тең деуін тап.
канондық тең деуін тап.
Тү зудің кез келген нү ктесін табу ү шін х = 0 деп аламыз, содан кейін осы мә нді берілген тең деулер жү йесіне қ оямыз.
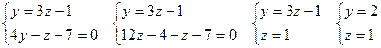 , т.е. А(0, 2, 1).
, т.е. А(0, 2, 1).
Тү зудің бағ ыттаушы векторының компоненттерін табамыз:
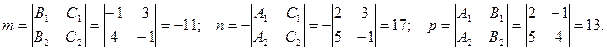
Сонда тү зудің канондық тең деуі:
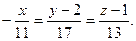
Мысал.
Тү зудің 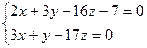 тең деуін канондық (жабайы) тү рге кеклтір.
тең деуін канондық (жабайы) тү рге кеклтір.
Жоғ арыдағ ы екі жазық тық тың қ иылысуы арқ ылы берілген тұ зудің кез келген нү ктесін табу ү шін z = 0 деп аламыз.Сонда:
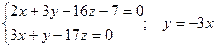 ;
;
2x – 9x – 7 = 0;
x = -1; y = 3;
Сонымен: A(-1; 3; 0).
Тү зудің бағ ыттаушы векторы: 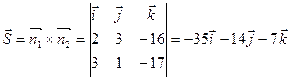 .
.
Сонымен: