
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Гипербола және оның қасиеттері
|
|
Анық тама. Гипербола деп фокустары деп аталатын нү ктелерден қ ашық тық тары айырмасының модулі сол фокустары арақ ашық тығ ынан (F1F2 = 2c) кем болатын тұ рақ ты 2 а санына тең болатын жазық тық тағ ы нү ктелердің геометриялық орнын айтады, оны былайша белгілейді:
|F1М - F2М| = 2 а (5).
F1, F2 – гиперболаның фокустары. F1 = (-c; 0); F2(c; 0), F1F2 = 2c.
с – фокустары ара қ ашық тығ ының жартысы; 2 а - тұ рақ ты шама. F1М жә не F2М қ ашық тық тарын r1 =F1М, r2= F2М деп белгілесек, онда (5) тең дік мына тү рде жазылады:
ï r1 – r2ï = 2a (51)
Гиперболаның бойынан кез келген М(х, у) нү кте алайық..
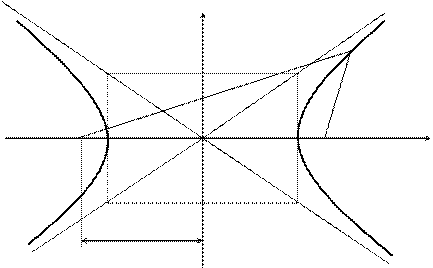 y
y
M(x, y)
b
r1
r2
x
a
F1 А2(- а; 0) А1(а; 0) F2
c
Сонда:
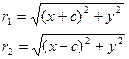
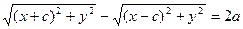
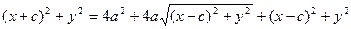
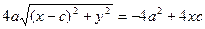
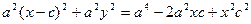
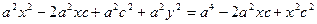
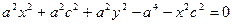
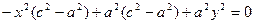
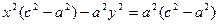
с2 – а2 = b2 деген белгілеме енгіземіз (геометриялық тү рдегі бұ л шама – кіші жарты ось)


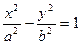
Гиперболаның жабайы (канондық) тең деуін алдық..
Гипербола фокустарын қ осатын кесіндінің ортасына (О нү ктеге), жә не координат осьтеріне қ арағ анда симметриялы.
2а гиперболаның нақ ты ө сі деп аталады.
2b гиперболаның жорамал ө сі деп аталады.
Гиперболаның қ асиеттерін студенттерге ө з беттерімен қ арастыруғ а тапсырылады.
 Гиперболаның екі асимптотасы болады жә не олар
Гиперболаның екі асимптотасы болады жә не олар 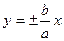 тең деулері арқ ылы беріледі.
тең деулері арқ ылы беріледі.
Анық тама. 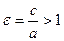 қ атынасы гиперболаның эксцентриситеті деп аталады, мұ ндағ ы с – фокустары қ ашық тығ ының жартысы, а –нақ ты жарты ө сь.
қ атынасы гиперболаның эксцентриситеті деп аталады, мұ ндағ ы с – фокустары қ ашық тығ ының жартысы, а –нақ ты жарты ө сь.
с2 – а2 = b2 екеніні ескерсек:
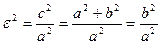
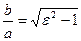
Егер а = b, 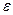 =
= 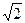 болса, онда гипербола тең бү йірлі (тең қ абырғ алы) деп аталады.
болса, онда гипербола тең бү йірлі (тең қ абырғ алы) деп аталады.
 Анық тама. Гиперболаның нақ ты ө сіне перпендикуляр, оның центріне қ арағ анда симметриялы жә не одан a/
Анық тама. Гиперболаның нақ ты ө сіне перпендикуляр, оның центріне қ арағ анда симметриялы жә не одан a/ 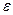 қ ашық тық та болатын екі тү зу гиперболаның директрисалары деп аталады.Олардың тең деулері:
қ ашық тық та болатын екі тү зу гиперболаның директрисалары деп аталады.Олардың тең деулері: 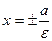 .
.
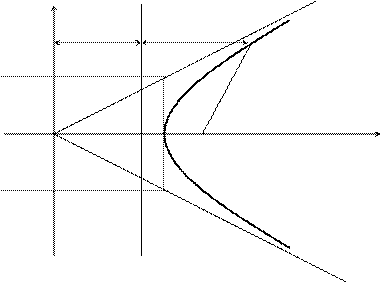
Теорема. Егер r – гиперболаның кез келген М нү ктесінен қ андай да бір фокусына дейінгі қ ашық тығ ы, ал d – осы фокусқ а сә йкес директрисағ а дейінгі қ ашық тығ ы болса, онда r/d қ атынас – эксцентриситетке тең тұ рақ ты шама.
Дә лелдеуі. Гиперболаны схемалық тү рде кескіндейік:
 y
y
a/e d
M(x, y)
r1
0 a F1 x
OF1 = c. Геометриялық кескінедемеден мыналарды жазуғ а болады:
a/ 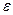 e + d = x, сондық тан d = x – a/
e + d = x, сондық тан d = x – a/ 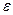 e. (x – c)2 + y2 = r2
e. (x – c)2 + y2 = r2
Гиперболаның канондық тең деуінен: 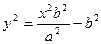 , с учетом b2 = c2 – a2:
, с учетом b2 = c2 – a2:
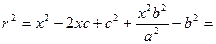
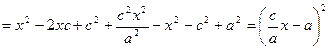

Сонда с/a = 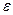 болғ андық тан, r =
болғ андық тан, r = 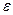 x – a.
x – a.
Сонымен: 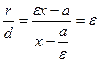 .
.
Гиперболаның сол жақ тағ ы тармағ ы ү шін дә лелдеме осы тә різдес.
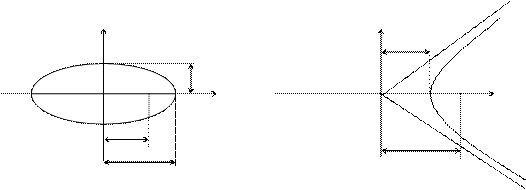
Пример. Тө белері мен фокустары  эллипсінің сә йкес тө белері мен фокустарында болатын гиперболаның тең деуін жаз.
эллипсінің сә йкес тө белері мен фокустарында болатын гиперболаның тең деуін жаз.
Эллипс ү шін: c2 = a2 – b2.
Гипербола ү шін: c2 = a2 + b2.
 |
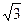

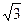
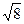
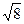
Гиперболаның тең деуі: 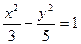 .
.
Мысал. Егер гиперболаның эксцентриситеті 2-ге тең, ал фокустары 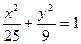 тең деуімен берілген эллипстің фокустарымен беттессе, онда гиперболаның тең деуін жаз.
тең деуімен берілген эллипстің фокустарымен беттессе, онда гиперболаның тең деуін жаз.
Шешу. Эллипстің фокустық ара қ ашық тығ ын табамыз: c2 = 25 – 9 = 16.
Гипербола ү шін: c2 = a2 + b2 = 16, 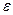 = c/a = 2; c = 2a; c2 = 4a2; a2 = 4;
= c/a = 2; c = 2a; c2 = 4a2; a2 = 4;
b2 = 16 – 4 = 12.
Сонда 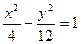 - гиперболаның тең деуі болады.
- гиперболаның тең деуі болады.