Парабола және оның қасиеттері

Анық тама. Парабола деп фокусы деп аталатын нү ктеден ара қ ашық тығ ы центрі арқ ылы ө тпейтін директрисасы деп аталатын берілген тү зуден бірдей ара қ ашық тық та болатын жазық тық тағ ы нү ктелердің жиынын айтады.

Координат басын фокус пен директрисаның ортасына орналастырамыз.

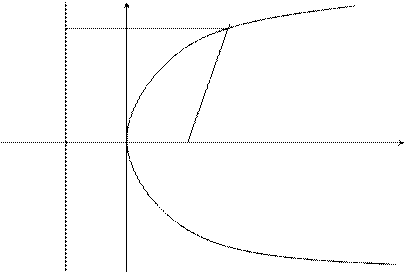у

А М(х, у)

О F x

p/2 p/2

р шама (фокустан директрисағ а дейінгі қ ашық тық) параболаның параметрі деп аталады. Параболаның жабайы тең деуін қ орытып шығ арайық.

Геометриялық кескіндемеден: AM = MF; AM = x + p/2;

MF² = y² + (x – p/2)²

(x + p/2)² = y² + (x – p/2)²

x² +xp + p²/4 = y² + x² – xp + p²/4

y² = 2px (*)

x = -p/2 - директрисаның тең деуі.

Параболаның қ асиеттері:

1. (*) тең деудегі у жұ п дә режелі болғ андық тан, парабола Ох ө сіне қ арағ анда симметриялы, Ох ө сі параболаның симметрия ө сі болады.
2. р> 0 болғ андық тан, (*) тең деуден х³ 0. Сондық тан, парабола Оу ө сінің оң жағ ында орналасады.
3. х = 0 болғ анда, у = 0. Демек, парабола координат басы арқ ылы ө теді.
4. х шектеусіз ө скен сайын у-тің модулі де шектеусіз ө седі. О(0; 0) нү кте параболаның тө бесі, Ғ М = г М нү ктесінің фокальдық радиусы болады.

y² = - 2px, х² = 2pу, х² = - 2pу (р> 0) тең деулері де параболаларды анық тайды.

Мысал. у² = 8х параболаның бойынан директрисағ а дейінгі қ ашық тығ ы 4 – ке тең болатын нү ктені тап.

Шешу. Параболаның тең деуінен р = 4 табамыз.

r = x + p/2 = 4; Сонда x = 2; y² = 16; y = ±4. Ізделінді нү ктелер: M₁(2; 4), M₂(2; -4).