Екі түзу арасындағы бұрыш. Параллельдік және перпендикулярлық шарттары. Нүктеден түзуге дейінгі қашықтығы

d₁ жә не d₂ тү зулері ө здерінің сә йкес жалпы тең деулері арқ ылы берілсін дейік:

А₁х+В₁у+С=0, А₂х+В₂у+С=0

Бұ рыштық коэффициенттері к₁= 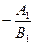, к₂=

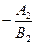
Егер d₁ ÷ ÷ d₂, онда к₁ = к₂.

Егер d₁ 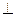d₂, онда к₁ = .

Екі тү зу арасындағ ы бұ аыш tg (Студенттердің ө з беттерімен қ орытуына беріледі)..

M(x₀, y₀) нү ктеден тү зуге дейінгі қ ашық тығ ы d= 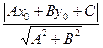(Студенттердің ө з беттерімен қ орытуына беріледі).

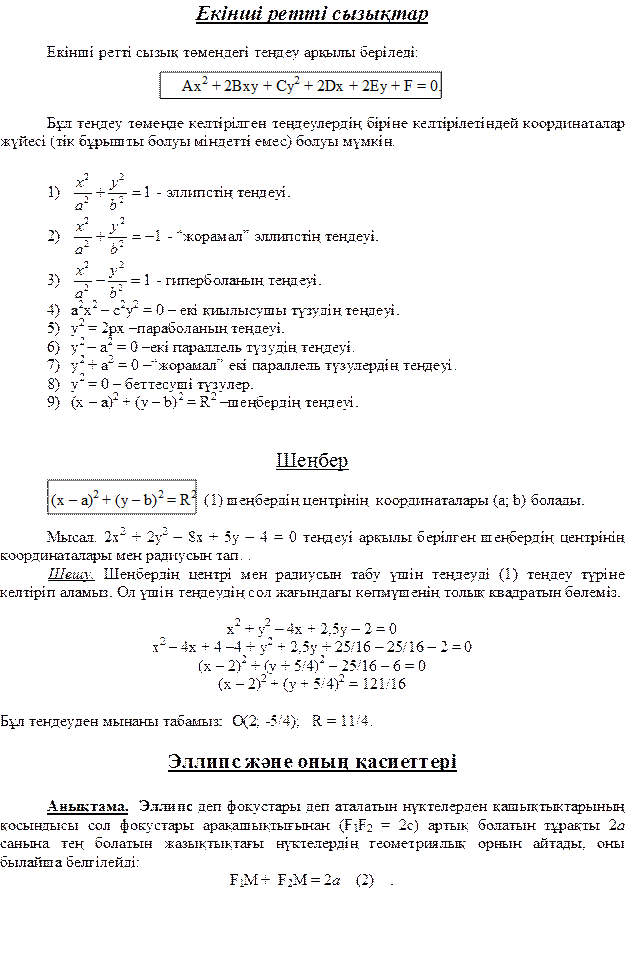
у

М

r₁

r₂

F₁ O F₂

F₁, F₂ – эллипстің фокустары. F₁ = (-c; 0); F₂(c; 0), F₁F₂ = 2c.

с – фокустары ар қ ашық тығ ының жартысы; 2 а - тұ рақ ты шама. F₁М жә не F₂М қ ашық тық тарын r₁ =F₁М, r₂= F₂М деп белгілесек, онда (2) тең дік мына тү рде жазылады:

r₁ + r₂ = 2 а (2¹)

Екі нү ктені ара қ ашық тығ ының формуласы бойынша: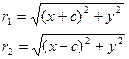

.

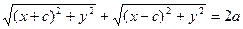Бұ л тең деуді тү рлендіріп, эллипстің жабайы (канондық) тең деуін табайық:

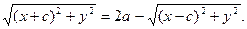
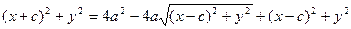
х ²+2сх+с²+ у² = 4а² – 4а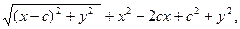

а тең діктің екі жағ ын а - ғ а бө ліп, квадраттайық:

х² -2сх +с²+у² = (а -

х² -2сх +с²+у² =

а²х²+а²у²+а²с²= а⁴ + с²х²,

(а²- с²) х²+а²у²+ = а² (а² - с²),

а> с болғ андық тан, а² - с²> 0 болады, сондық тан а² - с²= в² (3) деп белгілейміз.

Сонда в² х²+а²у²+ = а² в² шығ ады, осыдан 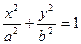(4), мұ ндағ ы х пен у -

эллипстің бойындағ ы кез келген нү ктелердің координаталары, а – эллипстің ү лкен жарты ө сі, в – оның кіші жарты ө сі. (4) тең деу эллипстің жабайы (канондық) тең деуі деп аталады.

Теорема. Эллипстің фокустық ара қ ашық тығ ы мен жарты ө стері мынадай қ атынас бойынша байланысады:

a² = b² + c².

Дэлелдеу: Егер М нү кте эллипстің вертикаль осьпен қ иылысу нү ктесінде болса, онда r₁ + r₂ = 2 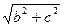(Пифагор теоремасы бойынша). Егер М нү кте эллипстің горизонталь осьпен қ иылысу нү ктесінде болса, онда r₁ + r₂ = a – c + a + c. Эллипстің

нық тамасы бойынша r₁ + r₂ – қ осынды тұ рақ ты шама, ендеше жоғ арыдағ ы екі тең дікті тең естіріп, мынадай тең дік аламыз:

a² = b² + c² .

Анық тама. 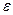= с/a қ атынас эллипстің эксцентриситеті деп аталады. с < a

болғ андық тан, 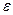< 1 болады.