
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ГЛОССАРИЙ. «Аналитикалық геометрия»
Стр 1 из 16Следующая ⇒
|
|
ПӘ ННІҢ ОҚ У-Ә ДІСТЕМЕЛІК КЕШЕНІ
«Аналитикалық геометрия»
В050109 – «Математика» мамандығ ы ү шін
ОҚ У -Ә ДІСТЕМЕЛІК МАТЕРИАЛДАР
Семей
Мазмұ ны
1 Глоссарийлар…………..…………………………………………………….3
2 Дә ріс оқ улар …………………………………………………………………5
3 Практикалық сабақ тар........…………………………………………………36
4 Студенттің ө здік жумысы...................………………………………………45
ГЛОССАРИЙ
| № | Жаң а ұ ғ ымдар | Мазмұ ны | |
| Екінші ретті анық тауыш | 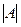 = det A = = det A = 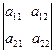 =а11а22 – а21а12 =а11а22 – а21а12
| ||
| Ү шінші ретті анық тауыш | 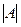 = det A = = det A = 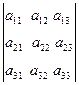 = а11 а22 а33 +а12 а11 а23 а31 +а13 а21 а32 -а13 а22 а31 -а12 а21 а33 -а11 а23 а32 = а11 а22 а33 +а12 а11 а23 а31 +а13 а21 а32 -а13 а22 а31 -а12 а21 а33 -а11 а23 а32
| ||
| Минор | М23= 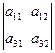
| ||
| Алгебралық толық тауыш | Аij=(-1)i+j 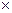 Mij Mij
| ||
| Матрица | . А= 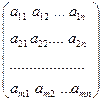
| ||
| Кері матрица | А-1  = = 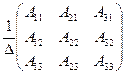 , , 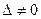
| ||
| Вектор | 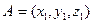 , , 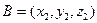
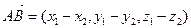 - вектордың координаталар. - вектордың координаталар.
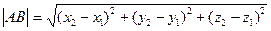 -АВ кесіндінің ұ зындығ ы -АВ кесіндінің ұ зындығ ы
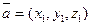 , , 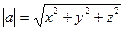 - вектордың ұ зындығ ы - вектордың ұ зындығ ы
| ||
| Скалярлық кө бейтіндісі | (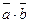 )= )= 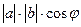 (
(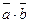 )= )= 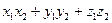 cos
cos 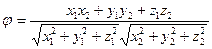 -Угол между векторами. -Угол между векторами.
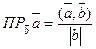 - проекция вектора - проекция вектора 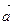 на вектор на вектор 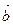 . .
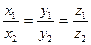 - условие коллинеарности векторов - условие коллинеарности векторов
| ||
| Векторлық кө бейтіндісі | 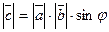 = Sпар.
с= = Sпар.
с=  = ( = (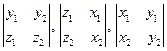 )
S= )
S= 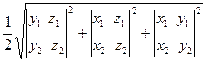 -ұ шбұ рыштын ауданы (векторлық кө бейтіндісінің геометриялық мағ ынасы) -ұ шбұ рыштын ауданы (векторлық кө бейтіндісінің геометриялық мағ ынасы)
| ||
| Смешанное произведение | (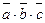 )= )= 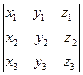 Егер (
Егер (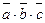 )=0, онда векторлар компланар болады.
V= )=0, онда векторлар компланар болады.
V= 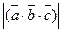 - параллелепипедтің кө лемі (аралас кө бейтіндісінің гелметриялық мағ ынасы) - параллелепипедтің кө лемі (аралас кө бейтіндісінің гелметриялық мағ ынасы)
| ||
| Жазақ тық тағ ы тү зудін тең деуі | Ах+Ву+С=0 – жалпы тең деу
к= 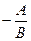 - бұ рыштық коэффициент - бұ рыштық коэффициент
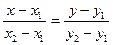 -екі нү ктеден ө тетін тү зудің тең деуі
A(x-x0)+B(y-y0)=0 – нормалі бар тү зудің тең деуі -екі нү ктеден ө тетін тү зудің тең деуі
A(x-x0)+B(y-y0)=0 – нормалі бар тү зудің тең деуі
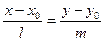 - бағ ыттылғ ан вектормен берілген тү зудің тең деуі
y-y0=k(x-x0) – бұ рыштық коэффициентпен берілген тү зудің тең деуі - бағ ыттылғ ан вектормен берілген тү зудің тең деуі
y-y0=k(x-x0) – бұ рыштық коэффициентпен берілген тү зудің тең деуі
 - кесінді арқ ылы тү зудің тең деуі
к1 = к2 – тү зулердің параллель шарты
к1 = - кесінді арқ ылы тү зудің тең деуі
к1 = к2 – тү зулердің параллель шарты
к1 =  - тү зулердің перпендикуляр шарты
tg - тү зулердің перпендикуляр шарты
tg  - тү зулердің арасындағ ы бұ рыш d= - тү зулердің арасындағ ы бұ рыш d= 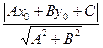 - нү ктеден тү зуге дейінгі қ ашық тық - нү ктеден тү зуге дейінгі қ ашық тық
| ||
| Екінші ретті қ исық тар | 1) 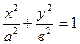 - эллипс, - эллипс, 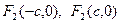 - фокустар, мұ ндағ ы - фокустар, мұ ндағ ы 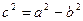 , , 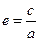 -эксцентриситет, -эксцентриситет, 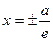 - директрисссалар
2) - директрисссалар
2) 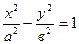 -гипербола, -гипербола, 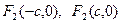 - фокустар, где - фокустар, где  , , 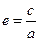 -эксцентриситет, -эксцентриситет, 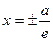 - директриссалар, - директриссалар, 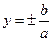 - асимптоталар
3) у2=2px жә не х2 =2ру –парабола, р – параболаның параметрі, - асимптоталар
3) у2=2px жә не х2 =2ру –парабола, р – параболаның параметрі, 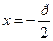 - директрисса, - директрисса, 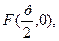 - параболаның фокусы - параболаның фокусы
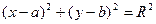 -шең бер, С(а, в) – шең бердің центрі, R – шең бердін радиусы. -шең бер, С(а, в) – шең бердің центрі, R – шең бердін радиусы.
| ||
| Кең істіктегі тұ зудің тең деудің | 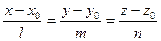 - тұ зудің канондық тең деуі, - тұ зудің канондық тең деуі, 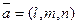 - бағ ыттылғ ан вектор - бағ ыттылғ ан вектор
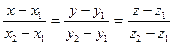 - екі нү ктеден ө тетін тузудің тең деуі - екі нү ктеден ө тетін тузудің тең деуі
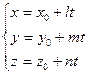 - тү зудің параметрлік тең деуі - тү зудің параметрлік тең деуі
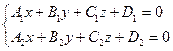 - уравнение прямой как пересечение двух плоскостей, где - уравнение прямой как пересечение двух плоскостей, где
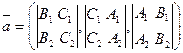 - бағ ыттылғ ан вектор - бағ ыттылғ ан вектор
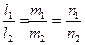 - тү зулердің параллель шарты l1l2+m1m2+n1n2=0– тү зулердің перпендикуляр шарты - тү зулердің параллель шарты l1l2+m1m2+n1n2=0– тү зулердің перпендикуляр шарты
| ||
| Жазық тық тың тең деуі | Ax+By+Cz+D=0 - Жалпы тең деуі
A(x-x0)+B(y-y0)+C(z-z0)=0, где 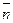 =(A, B, C) – жазық тық тың нормалі =(A, B, C) – жазық тық тың нормалі
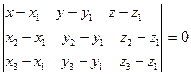 - Ү ш нуктедең ө тетін жазақ тық тын тең деуі
d= - Ү ш нуктедең ө тетін жазақ тық тын тең деуі
d=  - нү ктеден жазық тық қ а дейінгі қ ашық тық - нү ктеден жазық тық қ а дейінгі қ ашық тық
| ||