Кеңістікте нүкте мен бағыттаушы векторы арқылы берілген түзудің теңдеуі

Кез келген тү зу мен оғ ан параллель 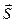(m, n, p) векторын алайық.. 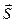векторы тү зудің бағ ыттаушы векторы деп аталады.

Тү зу бойынан кез келген М₀(x₀, y₀, z₀) жә не M(x, y, z) нү ктелерін аламыз..

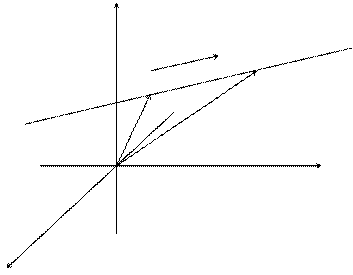z

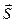M₁

M₀

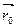
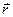
0 y

x

Бұ л нү ктелердің радиус- векторларын 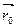и 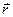арқ ылы белгілейік, сонда - = .

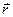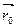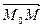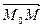и 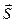векторлары коллинеар болғ андық тан, 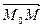= 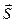t қ атынасы орындалады, мұ ндағ ы t – кез келген параметр.

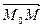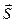= t тең діктен мынау шығ ады: 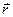- 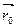= 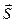t. Бұ дан 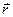= 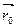+ 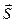t (2).

Бұ л тең деуді тү зудің кез келген нү ктесінің координаталары қ анағ аттандыратындық тан, (2) тең деу тү зудің параметрлік тең деуі болады.

Бұ л векторлық тең деу координаталық формада былайша жазылады:

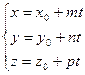
Бұ л жү йені тү рлендіріп t параметрге тең естіру арқ ылы кең істіктегі тү зудің канондық (жабайы) тең деуін аламыз:

.

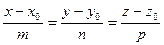Тү зудің параметрлік тең деуі канондық тең деуден шығ ады. Айталық бізге тү зудің канондық тең деуі берілсін. 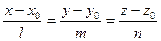(1). Осыны t параметрге тең естіреміз. Сонда:

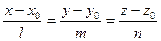=t, бұ дан 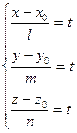, немесе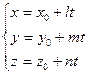

Анық тама. Тү зудің бағ ыттаушы косинустары деп 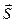векторының бағ ыттаушы косинустарын айтады жә не олар тө мендегі формулалар бойынша анық талады:

; .

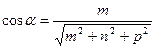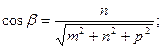
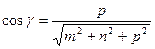Бұ дан мынаны аламыз: m: n: p = cosa: cosb: cosg.

m, n, p сандары тү зудің бұ рыштық коэффициенттері деп аталады. 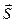- нө лдік емес вектор болғ андық тан, m, n и p бір уақ ытта нө лге тең бола алмайды, алайда бұ л сандардың біреу не екуі нө лге тең болуы мү мкін. Бұ л жағ дайда тү зудің тең деуінен сә йкес алымдарын нө лге тең естіруге тура келеді.