Начальные условия и задача Коши

Определение. Начальные условия для дифференциального уравнения 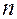-го порядка — это набор чисел

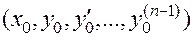, (2)

задающий для фиксированного значения независимой переменной 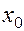значения неизвестной функции и ее производных вплоть до порядка, на единицу меньшего порядка уравнения:

.

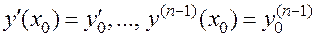Определение. Задачей Коши для дифференциального уравнения называется задача отыскания решения 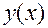, отвечающего заданным начальным условиям.

Геометрический смысл задачи Коши для дифференциального уравнения 1-го порядка

Для дифференциального уравнения 1-го порядка (при 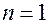) начальные условия (2) имеют вид пары чисел 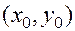. Тем самым ставится задача отыскания решения 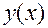, для которого . Геометрически это означает выбор из совокупности интегральных кривых той, которая проходит через заданную точку плоскости 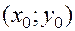(рис. 1).

Рис. 1