Однородное уравнение первого порядка

Определение. Однородным уравнением первого порядка называется уравнение, разрешенное относительно производной:

, (9)

в котором функция при всех вещественных 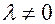удовлетворяет условию:

.

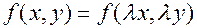Полагая в этом равенстве 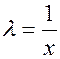, убеждаемся, что правая часть зависит только от отношения переменных : .

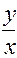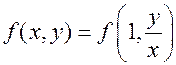Приведем примеры таких функций:

1) 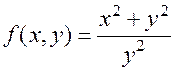; 2) 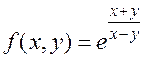. Напротив, функция 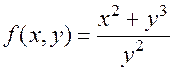, как легко проверить, не удовлетворяет условию .

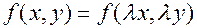Введем новую искомую функцию 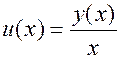, так что 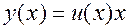. Тогда формула для производной произведения дает: 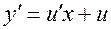, и уравнение (9) принимает вид:

—

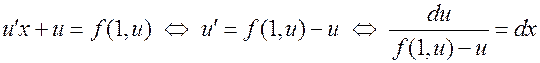уравнение с разделяющимися переменными относительно новой искомой функции 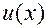. Если для него найден общий интеграл (методом, описанным в предыдущем разделе):

,

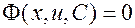то, заменяя в нем 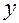на 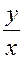, получим общий интеграл для исходной неизвестной функции :

.

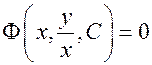Алгоритм решения однородного уравнения первого порядка:

1. Проверка однородности: .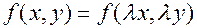

2. Введение новой искомой функции .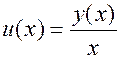

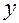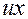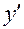3. Замена в уравнении на , на .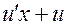

4. Решение полученного уравнения с разделяющимися переменными относительно .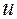

5. Замена в полученном общем интеграле 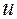на .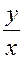

Пример. Решим уравнение 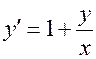. Здесь 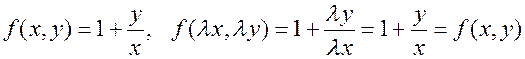, так что уравнение, действительно, является однородным. После введения новой переменной 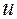получаем уравнение:

.

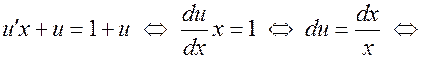
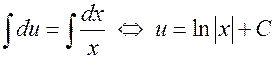Заменяя 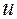на 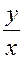, получаем общий интеграл для исходной неизвестной функции : .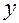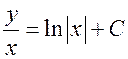