Общее решение и общий интеграл

Начальные условия 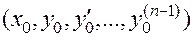, будучи набором из 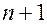чисел, задают точку пространства 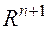. Множество всех рассматриваемых вариантов начальных условий образует некоторую область .

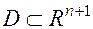Для различных видов ограничений на функцию 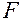и на область 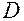имеет место существование и единственность решения задачи Коши для начальных условий из 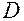. Приведем примеры соответствующих теорем.

I. Пусть уравнение 1-го порядка является разрешённым относительно производной :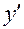

.

Теорема 1. Если функция и ее частная производная непрерывны в области 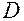плоскости , то решение задачи Коши для любых начальных условий 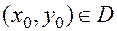существует и единственно в некоторой окрестности точки .

II. Пусть уравнение 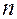-го порядка является разрешённым относительно старшей производной :

.

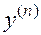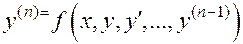Теорема 2. Если функция и ее частные производные 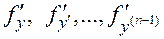непрерывны в области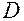 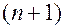-мерного пространства 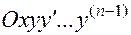, то решение задачи Коши для любых начальных условий 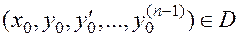существует и единственно в некоторой окрестности точки .

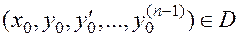В дальнейшем будем предполагать, что дифференциальные уравнения рассматриваются в области 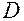существования и единственности решения.

Определение. Общим решением дифференциального уравнения 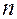-го порядка называется функция 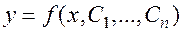, зависящая от аргумента 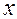и от 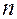произвольных постоянных 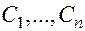, которая удовлетворяет двум условиям:

1) при любых значениях произвольных постоянных эта функция является решением;

2) за счет выбора значений произвольных постоянных можно получить решение задачи Коши для любых начальных условий из области существования и единственности решения.

Заметим, что количество произвольных постоянных равно порядку уравнения.

Определение. Частным решением дифференциального уравнения называется функция, которая получается из общего решения, если произвольным постоянным придать определенные значения.

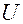Напомним определение неявной функции: функция в окрестности точки 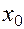, задана неявно уравнением 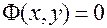, если при всех 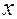из этой окрестности справедливо равенство .

Обычное, «явное» задание функции можно рассматривать как частный случай неявного: ; здесь .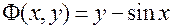

Определение. Общим интегралом дифференциального уравнения 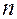-го порядка называется уравнение

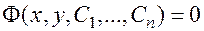, (3)

зависящее от 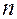произвольных постоянных 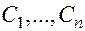, которое задает общее решение 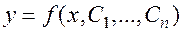как неявную функцию.

Определение. Частным интегралом называется уравнение, которое получается из общего интеграла (3), если произвольным постоянным придать определенные значения.

Замечание. В тех случаях, когда удается найти решение дифференциального уравнения, оно имеет, как правило, вид общего интеграла (3). Если при этом можно 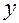явно выразить через 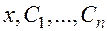(«разрешить уравнение относительно 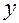»), то приходим к общему решению.