
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод функциональной подстановки
|
|
Метод функциональной подстановки является, пожалуй, самым распространенным методом решения сложных задач школьной математики. Суть метода состоит в введении новой переменной 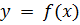 , применение которой приводит к более простому выражению. Частным случаем функциональной подстановки является тригонометрическая подстановка.
, применение которой приводит к более простому выражению. Частным случаем функциональной подстановки является тригонометрическая подстановка.
Основная трудность решения задач методом функциональной подстановки заключается в том, что зачастую трудно угадать вид самой подстановки и вид уравнений (или неравенств), где эту подстановку можно использовать. В настоящем разделе предлагаются наиболее распространенные уравнения и неравенства, которые эффективно решаются методом функциональной подстановки.
Задачи и решения
Пример 1.1. Решить уравнение
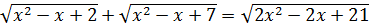 (1.1)
(1.1)
Решение. Введем новую переменную 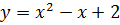 , тогда из (1.1) получаем уравнению
, тогда из (1.1) получаем уравнению 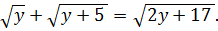 Поскольку обе части полученного уравнения неотрицательны, то после возведения в квадрат получаем равносильное уравнение
Поскольку обе части полученного уравнения неотрицательны, то после возведения в квадрат получаем равносильное уравнение  Отсюда вытекает
Отсюда вытекает  и
и 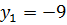 ,
, 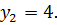
Рассмотрим два уравнения
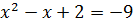 и
и 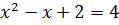 .
.
Первое уравнение корней не имеет, а из второго получаем 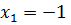 и
и 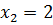 . Подстановкой в (1.1) убеждаемся в том, что найденные значения переменной
. Подстановкой в (1.1) убеждаемся в том, что найденные значения переменной 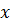 является корнями исходного уравнения.
является корнями исходного уравнения.
Ответ: 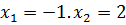
Пример 1.2. Решить уравнение
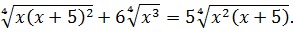
Решение. Нетрудно видеть, что 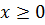 и
и 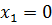 является корнем уравнения (1.2).
является корнем уравнения (1.2).
Пусть теперь 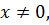 тогда части уравнения (1.2) разделим на
тогда части уравнения (1.2) разделим на 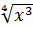 и получим уравнение
и получим уравнение
 (1.3)
(1.3)
Если обозначить  , то уравнение (1.3) принимает вид квадратного уравнения
, то уравнение (1.3) принимает вид квадратного уравнения 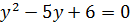 , корнями которого являются
, корнями которого являются  и
и 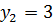 .
.
Рассмотрим уравнения 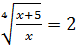 и
и 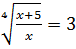 , откуда следует, что
, откуда следует, что 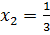 и
и 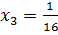 . Так как
. Так как 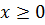 , то найденные значения x являются корнями уравнения (1.2).
, то найденные значения x являются корнями уравнения (1.2).
Ответ: 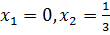 и
и 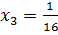 .
.
Пример 1.3. Решить уравнение
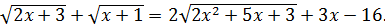 (1.4)
(1.4)
Решение. Перепишем уравнение (1.4) в виде
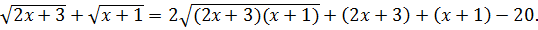 (1.5)
(1.5)
Положим, что 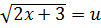 и
и 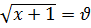 , тогда из (1.5) получим уравнение
, тогда из (1.5) получим уравнение  из которого следует
из которого следует 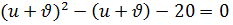 и
и  . Так как
. Так как  и
и 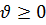 , то
, то  и при этом
и при этом 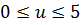 .
.
Поскольку 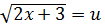 и
и 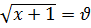 , то
, то 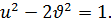 Отсюда получаем систему уравнений
Отсюда получаем систему уравнений
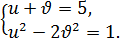 (1.6)
(1.6)
где 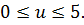 Решением системы уравнений (1.6) относительно u является
Решением системы уравнений (1.6) относительно u является 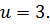 Так как при этом
Так как при этом 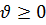 и
и 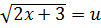 , то
, то 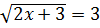 и
и 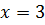 .
.
Ответ: 
Пример 1.4. Решить уравнение
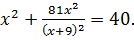 (1.7)
(1.7)
Решение. Для преобразования левой части уравнения (1.7) воспользуемся очевидным равенством  Тогда из уравнения (1.7) имеем
Тогда из уравнения (1.7) имеем
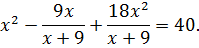
и
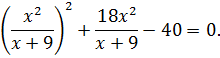
Если затем положить 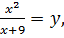 то получим уравнение
то получим уравнение 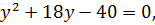 корни которого равны
корни которого равны 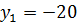 и
и 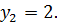
Таким образом, необходимо рассмотреть два уравнения 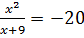 и
и 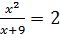 , т.е
, т.е 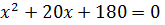 и
и 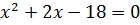 , где
, где 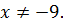 Первое уравнение корней не имеем, а из второго получаем
Первое уравнение корней не имеем, а из второго получаем  .
.
Ответ: 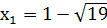 ,
, 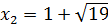 .
.
Пример 1.5. решить уравнение
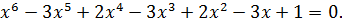 (1.8)
(1.8)
Решение. Первоначально убедимся, что 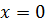 не является корнем уравнения (1.8).так как
не является корнем уравнения (1.8).так как 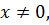 то разделим обе части уравнения (1.8) на
то разделим обе части уравнения (1.8) на  . Тогда получим
. Тогда получим
 . (1.9)
. (1.9)
Пусть  , тогда
, тогда
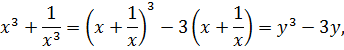
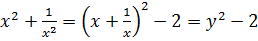 .
.
и из уравнения (1.9) следует 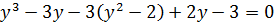 или
или 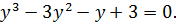 Последнее уравнение представим в виде
Последнее уравнение представим в виде 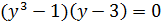 . Отсюда следует, что
. Отсюда следует, что 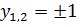 и
и 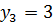 .
.
Далее, рассмотрим три уравнения  ,
, 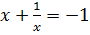 и
и 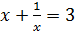 .
.
Первые два уравнения корней не имеют, а корнями третьего уравнения 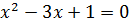 являются
являются 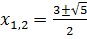
Ответ: 
Пример 1.6. Решить неравенство
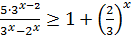 (1.10)
(1.10)
Решение. Разделим числитель и знаменатель дроби в левой части неравенства (1.10)  и обозначим
и обозначим  через
через 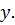 Тогда неравенство (1.10) можно переписать как
Тогда неравенство (1.10) можно переписать как
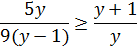
и
 (1.11)
(1.11)
Решая неравенство (1.11) с учетом того 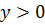 , получаем
, получаем 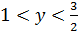 . Поскольку
. Поскольку 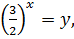 то
то 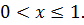
Ответ: 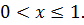
Пример 1.7. Решить уравнение
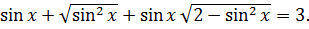 (1.12)
(1.12)
Решение. Выполним замену переменных, пусть 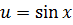 и
и 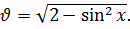 Так как
Так как 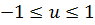 и
и 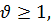 то
то 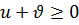 . Кроме того, имеем
. Кроме того, имеем 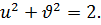
В таком случае из уравнения (1.12) получаем систему уравнений
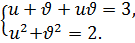 (1.13)
(1.13)
Пусть теперь  и
и 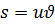 , тогда из системы уравнений (1.13) следует
, тогда из системы уравнений (1.13) следует 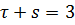 и
и 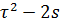 . Отсюда с учетом того, что
. Отсюда с учетом того, что 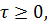 получаем
получаем 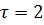 и
и 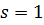 . Следовательно, имеет место
. Следовательно, имеет место 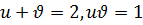 и
и 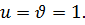
Поскольку 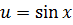 и
и  то
то 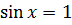 и
и 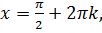 где
где 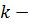 целое число.
целое число.
Ответ: 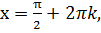 где
где 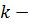 целое число.
целое число.