Задачи и решения. Пример 3.1.Доказать неравенство

Пример 3.1. Доказать неравенство

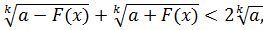(3.10)

где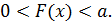

Доказательство. Преобразуем левую часть неравенства (3.10) с использованием неравенства (3.7), т.е.

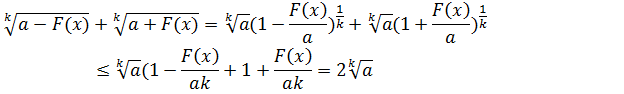
Так по условию 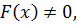то равенства в неравенстве Бернулли (3.7) не будет, поэтому доказано строгое неравенство (3.10).

Пример 3.2. Доказать, что если 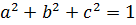, то

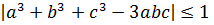(3.11)

Доказательство. Введем обозначения 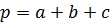и 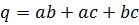. Тогда 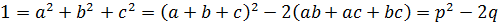и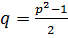

Используя неравенство Коши-Буняковского (3.8), можно записать 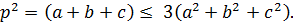Так как .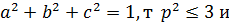

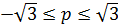Пусть 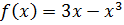. Для доказательства неравенства (3.11) требуется показать, что 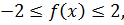где .

Так как 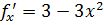, то корни уравнения 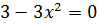являются точками, подозрительными на экстремум функции 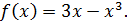Уравнение 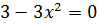имеет два корня: 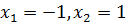. Поскольку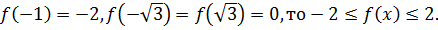

Отсюда следует, что неравенство (3.11) доказано.

Пример 3.3. Доказать, если 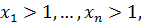то

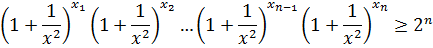
Доказательство. Для получения нижней оценки левой части требуемого неравенства первоначально воспользуемся неравенством Бернулли (3.6), а затем неравенством Коши (3.2), тогда

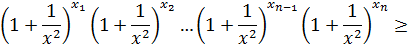
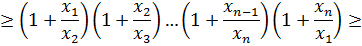
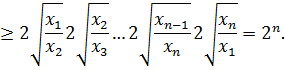
Пример 3.4. Решить уравнение

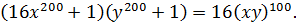(3.12)

Решение. Используя неравенство Коши (3.2), можно записать

т.е. имеет место неравенство

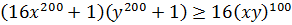
Отсюда и из уравнения (3.12) следует, что приведенные выше неравенства Коши обращаются в равенства. А это возможно лишь в том случае, когда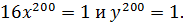

Следовательно, имеем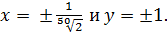

Ответ: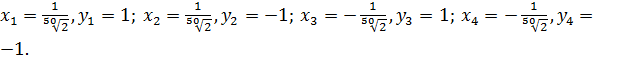

Пример 3.5. Решить уравнение

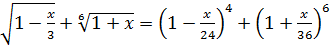(3.13)

Решение. Применим к левой части уравнения (3.13) неравенство Бернулли (3.7), а к правой части – неравенство (3.6), тогда

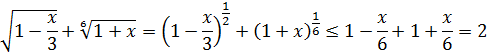
и

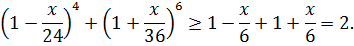
Отсюда следует, что неравенства Бернулли, примененные к обеим частям уравнения (3.13), обращаются в равенство, а это возможно лишь в том случае, когда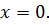

Ответ: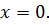

Пример 3.6. Доказать неравенство

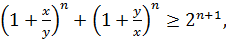(3.14)

где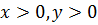

Доказательство. Непосредственно из неравенства (3.9) следует 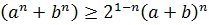. Используя это неравенство и неравенство Коши (3.3), получаем неравенство (3.14) следующим образом:

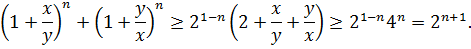
Пример 3.7. Доказать, что

(3.15)

где 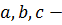стороны треугольника, а 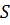- его площадь.

Доказательство. Известно, что 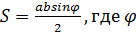- угол между сторонам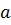и и 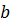. Поскольку 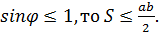Используя неравенство Коши 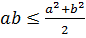, то получаем верхнюю оценку площади треугольник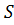а вида 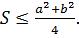По аналогии с изложенным выше имеет место 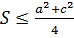и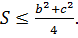

Тогда .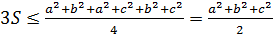

Отсюда следует справедливость неравенства (3.15).

Пример 3.8. Доказать, что для всякого прямоугольного параллелепипеда с ребрами 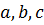и диагональю 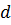имеет место неравенство

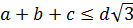(3.16)

Доказательство. Воспользуемся неравенством Коши-Буняковского (3.8), тогда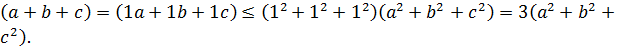

Поскольку в прямоугольном параллелепипеде 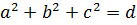(теорема Пифагора), то . Отсюда следует справедливость неравенства (3.16).

Заметим, что равенство (3.16) достигается тогда и только тогда, когда прямоугольный параллелепипед является кубом.

Пример 3.9. Пусть M – точка, лежащая внутри прямоугольника ABCD, и S – его площадь. Доказать, что

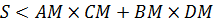(3.17)

Доказательство. Через точку , лежащую внутри прямоугольника , проведем 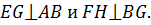Обозначим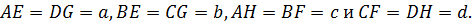

Тогда 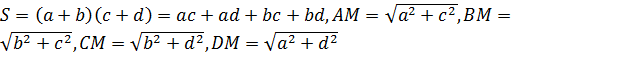и требуемое неравенство (3.17) принимает вид

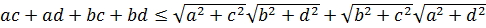(3.18)

Используя неравенство Коши-Буняковского (3.8), можно записать два неравенства

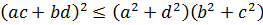
и

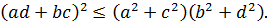
Следовательно, имеет место

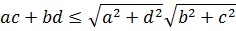
и

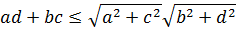
Складывая приведенные выше неравенства, получаем неравенство (3.18).