Задачи и решение

Пример 4.1. Решить уравнение

. (4.1)

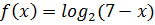Решение. Областью допустимых значений уравнения (4.1) являются . Рассмотрим функции и 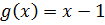. Известно, что функци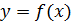я для являются убывающей, а функция 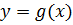– возрастающей. В этой связи уравнения(4.1) может иметь только один корень, т.е. 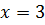, который легко находиться подбором.

Ответ:

Пример 4.2. Решить уравнение

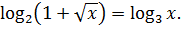(4.2)

Решение. Введем новую переменную 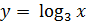. Тогда , 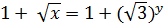и уравнения (4.2) принимает вид

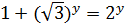(4.3)

Уравнение (4.3) имеет очевидной корень 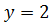. Покажем, что других корней нет. Для этого разделим обе части уравнения (4.3) на , тогда

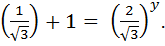(4.4)

Так как , а 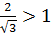, то левая часть уравнения (4.4) является убывающей функцией, а первая часть – возрастающей функцией. Поэтому уравнения (4.4) если имеет корень, так только один. Ранее было установлено, что 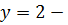корень уравнения (4.3). Следовательно, этот корень единственный.

Таким образом, имеем . Тогда единственный корнем уравнения (4.2) является .

Пример 4.3. Решить уравнение

(4.5)

Решение. Разделим обе части уравнения (4.5) на 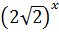, тогда

(4.6)

Подбором нетрудно установить, что является корнем уравнения (4.6). покажем, что других корней это уравнение не имеет.

Обозначим и . Очевидно, что 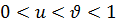. Следовательно, каждая из функци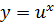й и 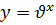является убывающей и при этом .

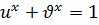Если , то , и .

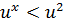Если , то , и .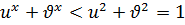

Следовательно, среди или корней уравнения (4.6) нет.

Ответ: