Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы, основанные на применении векторов
|
|
Недостаточное внимание в общеобразовательной школе уделяется применению векторов для решения уравнений и неравенств. Тем не менее, как будет показано ниже, в ряде случаев применение свойств векторов позволяет эффективно решать довольно-таки сложные уравнения и неравенства.
Вектора 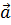 в трехмерном пространстве характеризуется тремя координатами
в трехмерном пространстве характеризуется тремя координатами 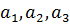 и модуль (длина) вектора
и модуль (длина) вектора 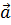 вычисляется по формуле
вычисляется по формуле 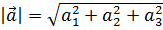 . Суммой (разностью) двух векторов
. Суммой (разностью) двух векторов 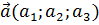 и
и 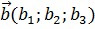 называется вектор
называется вектор 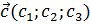 , координаты которого вычисляются как
, координаты которого вычисляются как  ,
, 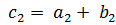 ,
, 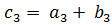 (соответственно,
(соответственно, 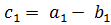 ,
, 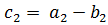 ,
, 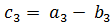 ).
).
Два различных от нуля вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. У коллинеарных векторов соответствующие координаты пропорциональны. Верно и обратное утверждение: если у двух векторов соответствующие координаты пропорциональны, то векторы коллинеарные.
Для векторов 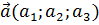 и
и 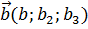 справедливо неравенство
справедливо неравенство 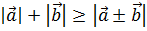 , т.е.
, т.е.
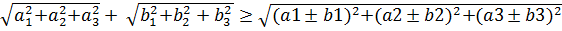 . (6.1)
. (6.1)
Формула (6.1) обобщается на случай суммы (или разности) трех и более векторов. Геометрический смысл (6.1) состоит в том, что длина ломанной линии, соединяющей две точки трехмерного пространства, больше или равна длине отрезка прямой, проведенного между этими точками. Формула (6.1) иначе называется неравенством треугольника.
Следует особо отметить, что равенство в (6.1) достигает тогда и только тогда, когда векторы 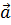 и
и 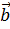 коллинеарные. В частности, из равенства в (6.1) следует, что
коллинеарные. В частности, из равенства в (6.1) следует, что 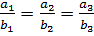 .
.
Причем равенство 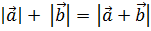 имеет место тогда и только тогда, когда векторы
имеет место тогда и только тогда, когда векторы 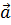 и
и 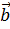 сонаправлены, т.е.
сонаправлены, т.е. 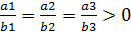 .
.
В свою очередь, равенство 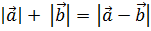 свидетельствует о том, что векторы
свидетельствует о том, что векторы 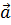 ,
, 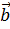 противоположно направлены
противоположно направлены 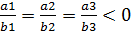 .
.
Скалярным произведением 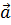 ·
· 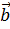 векторов
векторов 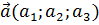 и
и 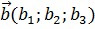 называется число(скаляр), которое вычисляется по формуле
называется число(скаляр), которое вычисляется по формуле
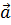 ·
· 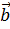 =
= 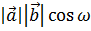 , (6.2)
, (6.2)
где 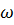 – угол, образованный векторами
– угол, образованный векторами 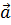 и
и 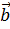 .
.
Для вычисления скалярного произведения двух векторов 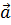 и
и 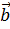 , заданных в координатной форме, существует еще одна формула
, заданных в координатной форме, существует еще одна формула
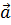 ·
· 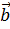 =
= 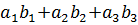 (6.3)
(6.3)
Из формул (6.2) и (6.3) легко получить формулу для вычисления косинуса угла.. между векторами 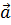 и
и 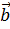 , т.е.
, т.е.
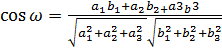 (6.4)
(6.4)
Из формулы (6.2) следует, что векторы 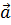 ,
, 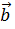 являются коллинеарными тогда и только тогда, когда
являются коллинеарными тогда и только тогда, когда 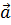 ·
· 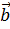 =
= 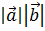 .
.
Отметим. Что формулы (6.1) 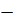 (6.4) обобщаются на случай векторов
(6.4) обобщаются на случай векторов 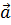 и
и 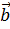 , заданных в n-мерном пространстве (где n
, заданных в n-мерном пространстве (где n 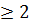 ).
).
Задачи и решения
Пример 6.1. Доказать, если 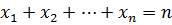 , то
, то
 (6.5)
(6.5)
где 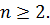
Доказательство. Пусть 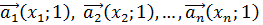 , тогда
, тогда 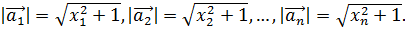 Введем в рассмотрение вектор
Введем в рассмотрение вектор 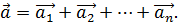
Так как 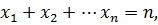 то вектор
то вектор 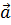 имеет координаты
имеет координаты  и
и 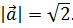 Поскольку
Поскольку 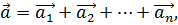 то неравенство треугольника принимает вид
то неравенство треугольника принимает вид
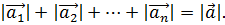 (6.6)
(6.6)
Если в неравенство (6.6) подставить выражения для 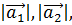 …,
…, 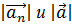 , то получим требуемое неравенство (6.5).
, то получим требуемое неравенство (6.5).
Пример 6.2. Решить неравенство
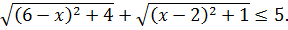 (6.7)
(6.7)
Решение. Пусть на плоскости вектор 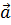 имеет координаты
имеет координаты 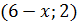 , а вектор
, а вектор 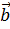 - координаты
- координаты 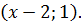 Тогда имеем
Тогда имеем 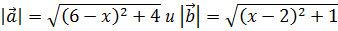 . Пусть
. Пусть 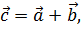 тогда координаты вектора
тогда координаты вектора 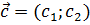 будут вычисляться по формулам
будут вычисляться по формулам 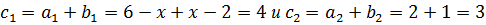 . Отсюда следует, что
. Отсюда следует, что 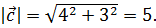 Поскольку
Поскольку 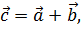 то имеет место неравенство треугольника
то имеет место неравенство треугольника 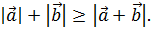 Если в последнее неравенство подставить выражения для
Если в последнее неравенство подставить выражения для 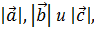 то получим неравенство
то получим неравенство 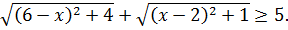 Отсюда и из (6.7) следует равенство
Отсюда и из (6.7) следует равенство
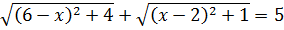 (6.8)
(6.8)
Равенство (6.8) означает, что 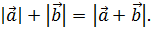
Отсюда следует, что векторы 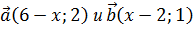 коллинеарные. Используя основное свойство коллинеарных векторов, получаем уравнение
коллинеарные. Используя основное свойство коллинеарных векторов, получаем уравнение 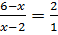 , откуда вытекает
, откуда вытекает 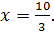
Ответ: 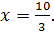
Пример 6.3. Решить уравнение
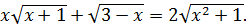 (6.9)
(6.9)
Решение. Введем в рассмотрение два вектора 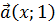 и
и 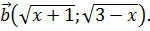 Тогда
Тогда 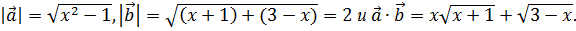
Принимая во внимание уравнение (6.9), получаем равенство 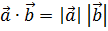 , наличие которого свидетельствует о том, что векторы
, наличие которого свидетельствует о том, что векторы 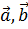 являются коллинеарными. Следовательно, имеет место уравнение
являются коллинеарными. Следовательно, имеет место уравнение
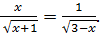 (6.10)
(6.10)
Из уравнения (6.10) следует, что 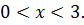 Если возвести в квадрат обе части уравнения (6.10), то получим уравнении
Если возвести в квадрат обе части уравнения (6.10), то получим уравнении 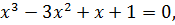
которое имеет следующих три корня: 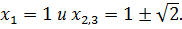 Поскольку
Поскольку 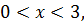 то решением уравнения (6.9) являются
то решением уравнения (6.9) являются 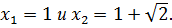
Ответ: 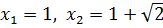 .
.
Пример 6.4. Найти минимальное значение функции
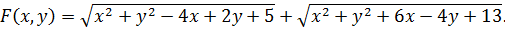
Решение. Представим функцию 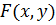 в виде
в виде
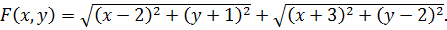 (6.11)
(6.11)
Введем на плоскости векторы 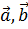 с координатами
с координатами 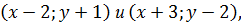 соответственно. Так как
соответственно. Так как 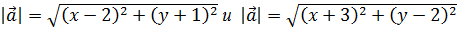 , то из выражения (6.11) следует, что
, то из выражения (6.11) следует, что 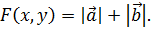
Пусть 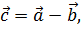 тогда координатами вектора
тогда координатами вектора 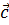 являются (-5; 3) и
являются (-5; 3) и 
Так как 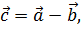 то
то 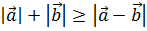 и
и  Теперь необходимо показать, что полученная нижняя оценка функции
Теперь необходимо показать, что полученная нижняя оценка функции 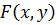 принимает значение
принимает значение 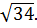
Если 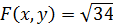 , то
, то 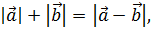 т.е. векторы
т.е. векторы  коллинеарные. Отсюда следует, что
коллинеарные. Отсюда следует, что 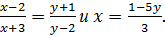 Положим
Положим 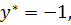 тогда
тогда 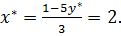 Если найденные значения
Если найденные значения 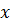 и
и 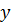 подставить в (6.11), то
подставить в (6.11), то 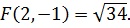 Следовательно, минимальное значение функции
Следовательно, минимальное значение функции 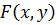 равно
равно 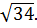
Ответ: