
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задачи и решения. Пример 8.1.Решить уравнение
|
|
Пример 8.1. Решить уравнение
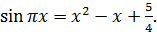 (8.1)
(8.1)
Решение. Выделим полный квадрат в правой части уравнения, т.е. 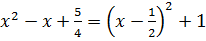 . Отсюда следует, что
. Отсюда следует, что 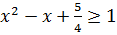 . Так как при этом
. Так как при этом 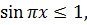 то из (8.1) получаем систему уравнений
то из (8.1) получаем систему уравнений
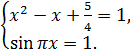 (8.2)
(8.2)
Решением второго уравнения системы является 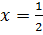 . Подстановкой в первое уравнение убеждаемся, что найденное значение x является решением системы уравнений (8.2).
. Подстановкой в первое уравнение убеждаемся, что найденное значение x является решением системы уравнений (8.2).
Ответ: 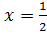 .
.
Пример 8.2. Решить уравнение
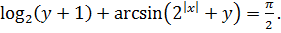 (8.3)
(8.3)
Решение. Обозначим 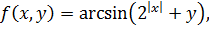 тогда из определения обратной тригонометрической функции
тогда из определения обратной тригонометрической функции 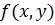 имеем
имеем 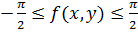 и
и  .
.
Так как 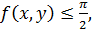 то из уравнения (8.3) следует неравенство
то из уравнения (8.3) следует неравенство 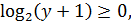 т.е
т.е 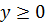 . Поскольку
. Поскольку  и
и 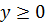 , то
, то 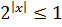 и
и 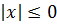 . Однако
. Однако 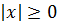 и поэтому
и поэтому 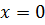 .
.
Если  и
и 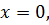 то
то 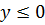 . Так как ранее было установлено, что
. Так как ранее было установлено, что 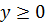 , то
, то 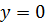 .
.
Ответ: 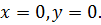
Пример 8.3. Решить уравнение
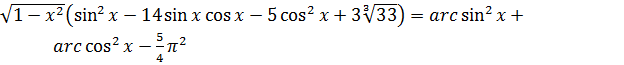 (8.4)
(8.4)
Решение. Областью допустимых значений уравнения (8.4) являются 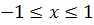 .
.
Первоначально покажем, что функция 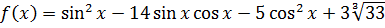 при любых
при любых 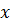 может принимать только положительные значения.
может принимать только положительные значения.
Представим функция 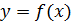 следующим образом:
следующим образом: 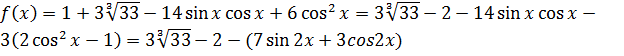 .
.
Поскольку 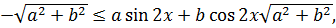 то имеет место
то имеет место 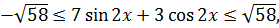 т.е
т.е 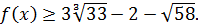
Следовательно для доказательство неравенства 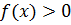 , необходимо показать, что
, необходимо показать, что 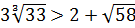 . С этой целью возведем в куб обе части данного неравенства, тогда
. С этой целью возведем в куб обе части данного неравенства, тогда
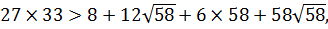
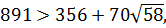
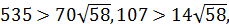
 ,
, 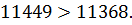
Полученное числовое неравенство свидетельствует о том что 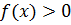 . Если при этом еще учесть, что
. Если при этом еще учесть, что 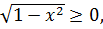 то левая часть уравнения (8.4) неотрицательна.
то левая часть уравнения (8.4) неотрицательна.
Рассмотрим теперь первую часть уравнения (8.4).
Так как 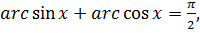 то
то
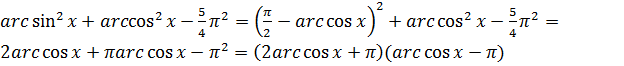 .
.
Однако известно, что 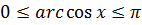 . Отсюда следует, что
. Отсюда следует, что 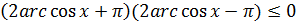 , т.е первая часть уравнения (8.4) не превосходить
, т.е первая часть уравнения (8.4) не превосходить 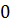 . Ранее было доказано, что левая часть уравнения (8.4) неотрицательна, поэтому равенство в (8.4) может быть только в том случае, когда обе его части равны
. Ранее было доказано, что левая часть уравнения (8.4) неотрицательна, поэтому равенство в (8.4) может быть только в том случае, когда обе его части равны 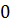 , а это возможно лишь при
, а это возможно лишь при 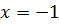 .
.
Ответ: 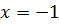 .
.