Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задачи и решения. Пример 9.1. Решить систему уравнений
|
|
Пример 9.1. Решить систему уравнений
 (9.5)
(9.5)
Решение. Если к обеим части каждого уравнения системы (9.5) прибавить 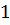 , то получаем
, то получаем
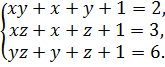 и
и 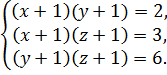
Из последней системы уравнений следует
 и
и 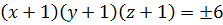
Пусть 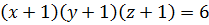 , тогда
, тогда
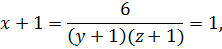
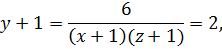
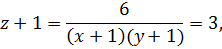
и 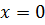 ,
, 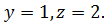
Если 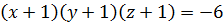 , то по аналогии с предыдущим получаем
, то по аналогии с предыдущим получаем 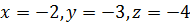 .
.
Ответ: 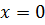 ,
, 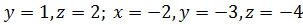 .
.
Пример 9.2. Решить систему уравнений
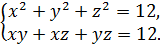 (9.6)
(9.6)
Решение. Из первого уравнения системы (9.6) вычем второго уравнение, тогда 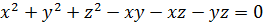 . Умножим на 2 обе части последнего уравнения и получим
. Умножим на 2 обе части последнего уравнения и получим
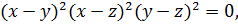
откуда следует 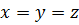 . В током случае первое уравнение системы (9.6) принимает
. В током случае первое уравнение системы (9.6) принимает 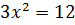 . Следовательно,
. Следовательно, 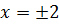 . Так как
. Так как 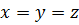 , то
, то
Ответ: 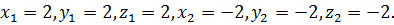
Пример 9.3. Решить систему уравнений
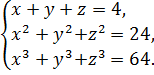 (9.7)
(9.7)
Решение. Обозначим 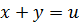 и
и 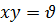 . Тогда из первого уравнения системы (9.7) следует, что из
. Тогда из первого уравнения системы (9.7) следует, что из 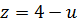 .
.
Преобразуем второе и третье уравнения системы (9.7) следующим образом:
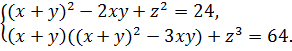
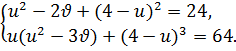
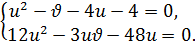
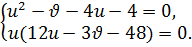 (9.8)
(9.8)
Из второго уравнения системы (9.8) следует, что необходимо рассмотреть два случая.
1) Пусть 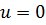 . Тогда
. Тогда 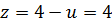 , а из первого уравнения системы
, а из первого уравнения системы
(9.8) получаем 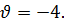 Так как
Так как 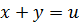 и
и 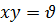 , то имеет место система уравнений
, то имеет место система уравнений
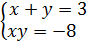 ,
,
из которой следует  и
и 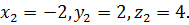
2) Пусть 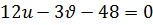 , тогда
, тогда 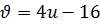 . Если данное выражение для
. Если данное выражение для  подставить в первое уравнение системы (9.8), то получим квадратное уравнение относительно переменной
подставить в первое уравнение системы (9.8), то получим квадратное уравнение относительно переменной 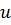 вида
вида 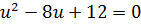 , которое имеет два корня
, которое имеет два корня 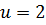 и
и 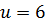 .
.
Если 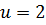 , то
, то 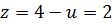 и из первого уравнения системы (9.8) получаем
и из первого уравнения системы (9.8) получаем 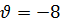 . В таком случае
. В таком случае
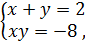
и 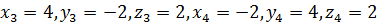 .
.
Если 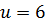 , то
, то 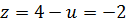 ,
, 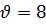 и
и
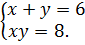
Отсюда следует 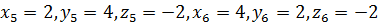 .
.
Ответ: См. выше.
Пример 9.4. При каких значениях параметра 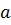 система неравенств
система неравенств
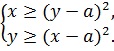 (9.9)
(9.9)
имеет единственное решение?
Решение. В систему неравенств (9.9) переменные 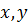 входят симметрично, поэтому единственное ее решение необходимо искать в виде
входят симметрично, поэтому единственное ее решение необходимо искать в виде 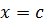 и
и 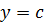 , где
, где 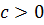 .
.
Подставим 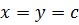 в любое из неравенств системы (9.9), тогда
в любое из неравенств системы (9.9), тогда 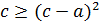 или
или 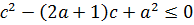 . Для того, чтобы квадратное неравенство имело бы единственное решение, необходимо его дискриминант приравнять нулю, т.е.
. Для того, чтобы квадратное неравенство имело бы единственное решение, необходимо его дискриминант приравнять нулю, т.е. 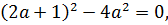
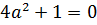 и
и 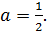
Ответ: