Задачи и решений

Пример 10.1. Решить уравнение

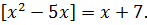(10.3)

Решение. Поскольку 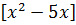являются целым числом, то 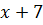- тоже целое число. Следовательно, число 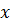также является целым. В таком случае 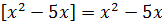и уравнение (10.3) принимает вид 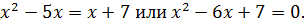Целыми корнями последнего уравнения являются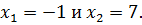

Ответ: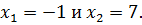

Пример 10.2. Решить уравнение

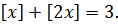(10.4)

Решение. Рассмотрим последовательно три случая.

Если 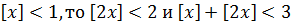, т.е. решением уравнения (10.4) могут быть только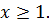

Пусть 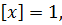тогда из уравнения (10.4) следует, что 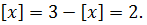Так как 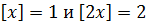, то получаем систему неравенств

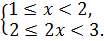
Решением данной системы неравенств являются .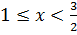

Если 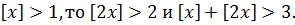Следовательно, уравнение (10.4) не имеет корней среди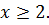

Ответ: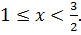

Пример 10.3. Решить уравнение

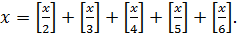(10.5)

Решение. Используя свойство (10.2), можно записать

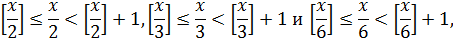
Так как 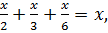то, складывая почленно три приведенные выше неравенства, получим

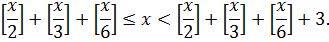
Отсюда, принимая во внимание уравнение (10.5), следуют неравенства

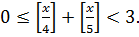(10.6)

Поскольку в этом случае 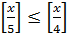следует, что 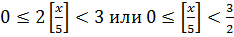. Так как 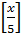- целое число, то отсюда получаем, что 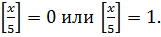Следовательно, имеем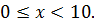

Из уравнения (10.5) следует, что 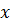– целое число. Так как 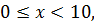то остается лишь проверить целые значения 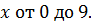Нетрудно установить, что решениями (10.5) являются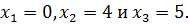

Ответ: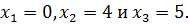

Пример 10.4. Решить уравнение

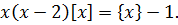(10.7)

Решение. Из формулы (10.1) следует, что 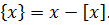В этой связи уравнение (10.7) можно переписать, как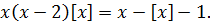

Отсюда следует уравнение

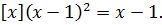(10.8)

Очевидно, что 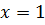является корнем уравнения (10.8). Положим, что 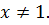Тогда разделим обе части уравнения (10.9) на 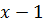и получим уравнение

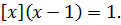(10.9)

Рассмотрим последовательно несколько случаем.

Если 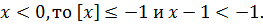В таком случае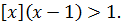

Если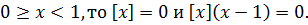

Если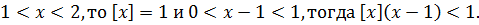

Если 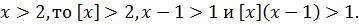Отсюда следует, что уравнение (10.9) корней не имеет.

Следовательно, уравнение (10.7) имеет единственный корень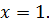

Ответ: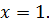

Пример 10.5. Решить уравнение

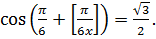(10.10)

Решение. Решая тригонометрическое уравнение (10.10), получаем

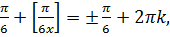_­(10.11)

где 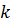– целое число. Из уравнения (10.11) получаем совокупность двух уравнений 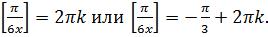Левые части обоих уравнений являются целыми числами, в то время как их правые части (за исключением случая 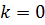в первом уравнении) принимают иррациональные значения.

Следовательно, равенство в уравнениях совокупности может иметь место только в том случае, когда правые их части являются рациональными (точнее, целыми) числами. А это возможно лишь в первом уравнении при условии, что 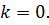В этом случае получаем уравнение 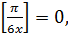откуда следует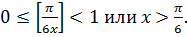

Ответ: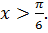

Пример 10.6. Решить уравнение

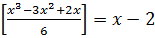(10.12)

Решение. Левая часть уравнения (10.12) принимает только целые значения, поэтому число 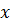является целым.

Так как 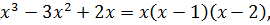то при любом целом 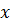многочлен 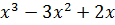представляет собой произведение трех последовательно расположенных на числовой оси 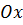целых чисел, среди которых имеется хотя бы одно четное число и число, кратное трем. Следовательно, многочлен делится на 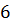без остатка, т.е. 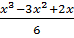является целым числом.

В этой связи 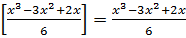и уравнение (10.12) принимает вид 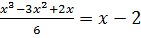или

(10.13)

Так как 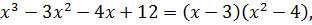то корнями уравнения (10.13) являются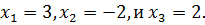

Ответ: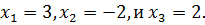

Пример 10.7. Доказать равенство

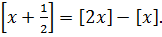(10.14)

для произвольного действительного числа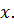

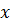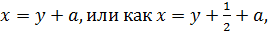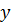Доказательство. Любое число можно представить или как где - целое число и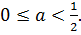

Рассмотрим два возможных случая.

1) Пусть 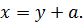Так как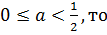

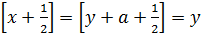и

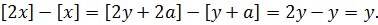
2) Пусть 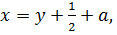тогда

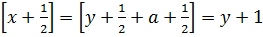и

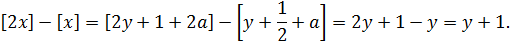
Таким образом, равенство (10.14) выполняется для каждого из двух рассмотренных выше случаем. Следовательно, равенство (10.14) доказано.

Заключение

В результате работы над дипломным проектом был проведен анализ решения нестандартных типов решения тестовых задач. Все рассмотренные задачи, решаемые нестандартными методами, классифицированы по следующим типам:

1. метод функциональной подстановки

2. методы, основанные на применении численных неравенств,

3. метод тригонометрической подстановки;

4. методы, основанные на монотонности функций,

5. методы решения функциональных уравнений,

6. методы, основанные на применении векторов,

7. комбинированные методы,

8. методы, основанные на использовании ограниченности функций,

9. методы решения симметрических систем уравнений,

10. методы решения уравнений, содержащих целые или дробные части числа.

В каждом из этих типов рассмотрены конкретные примеры и методы их решения.

Материал, содержащийся в дипломной работе, представляет собой основу методического пособия, которое можно при определенной доработке, внедрять как в школьный процесс, так и при подготовке абитуриентов к поступлению.