Задачи и решения. Пример 7.1. Решить уравнение

Пример 7.1. Решить уравнение

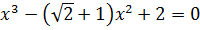(7.1)

Решение. Рассмотрим уравнение с параметром a вида

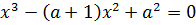(7.2)

которое совпадает с уравнением (7.1) при 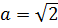. Перепишем уравнение (7.2)в виде квадратного уравнения относительно неизвестной переменной a, т.е.

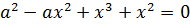(7.3)

Решением уравнения (7.3) относительно a являются

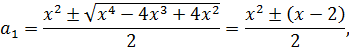
т.е. 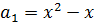и 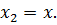Поскольку 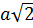, то получаем два уравнения относительно переменой вида 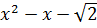и 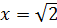. Отсюда получаем три корня исходного уравнения (7.1), т.е. 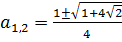и .

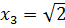Ответ: , .

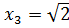Пример 7.2. Решить уравнение

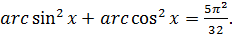(7.4)

Решение. Обозначим 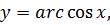тогда 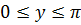. Известно, что 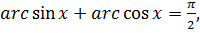тогда 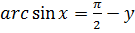и из уравнения (7.4) получаем уравнение относительно переменной 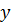вида 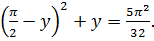Решая последнее уравнение, получаем и 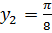. Таким образом, имеет место 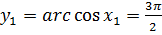и 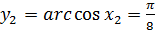. Отсюда следует 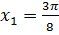и .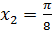

Пример 7.3. Найти все значения 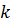, при которых разрешимо уравнение

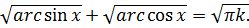(7.5)

Решение. Воспользуемся известным тригонометрическим равенством 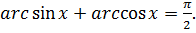Обозначим 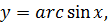тогда и из (7.5) получаем

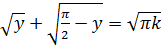(7.6)

где .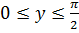

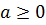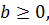Воспользуемся неравенствами, которые имеют место для произвольных и вида

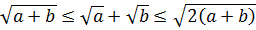
(данные неравенство легко доказать самостоятельно).

Следовательно, 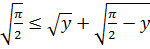и из (7.6) получаем 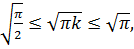откуда следует .

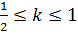Ответ: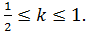

Пример 7.4. Решить уравнение

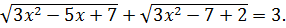(7.7)

Решение. Преобразуем уравнение (7.7) согласно известного равенства 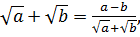где 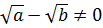, тогда 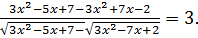отсюда следует

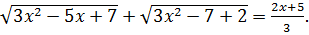(7.8)

Если уравнение (7.7) сложить с уравнением (7.8), то получаем 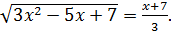Поскольку левая часть уравнения неотрицательна, то 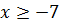. Возведем обе части уравнения в квадрат, тогда получаем квадратное уравнение 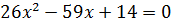, корнями которого являются 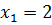и 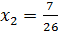. Непосредственной подстановкой в (7.7) убеждаемся, что найденные значения 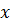являются его корнями.

Ответ: , .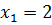

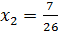Пример 7.5. Решить уравнение

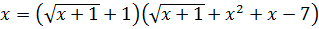. (7.9)

Решение. Очевидно, что областью допустимых значений уравнения (7.9) являются 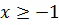. Умножим обе части уравнения (7.9) на 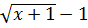, тогда получаем

,

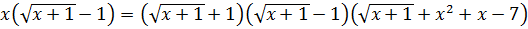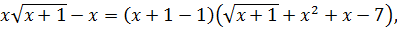
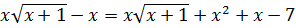
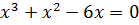. (7.10)

Решением уравнения (7.10) являются 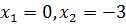и .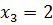

Однако 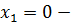посторонний корень для уравнения (7.9), поскольку при этом значении 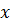левая часть уравнения (7.9) равна 0, а правая меньше 0. Так как 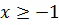, то 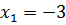не может быть корнем уравнения (7.9). в этой связи 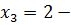единственное решение исходного уравнения (7.9).

Пример 7.6. Решить уравнение

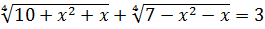. (7.11)

Решение. Обозначим 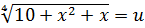и 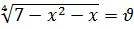, тогда из уравнения (7.11) получаем систему двух уравнений относительно переменных 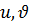вида

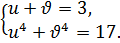(7.12)

Где 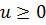и .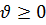

Преобразуем левую часть второго уравнения системы (7.12) следующим образом:

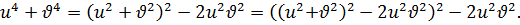
Так как 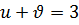, то 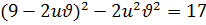. Отсюда получаем 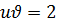или 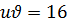. Рассмотрим две системы

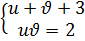и

Корням первой системы являются 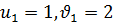и 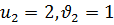, а вторая система решение не имеет.

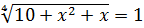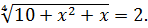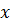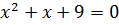Следовательно или Отсюда получаем два уравнения относительно переменной вида и 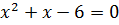. Первое уравнений корней не имеет, а из второго следует 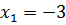и .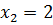

Ответ: , .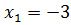

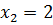Пример 7.7. Решить уравнение

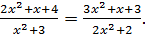(7.13)

Решение. Преобразуем уравнение (7.13), используя свойство пропорции: если 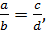то 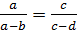. Тогда уравнение (7.13), можно переписать как

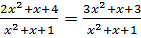. (7.14)

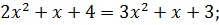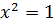Поскольку то из уравнения (7.14) получаем т.е. и .

Так как уравнения (7.13) и (7.14) равносильны, то решением уравнения (7.13) являются 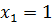и .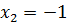

Пример 7.8. Доказать неравенство

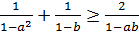. (7.15)

где .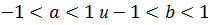

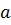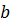Доказательство. Доказательство неравенства (7.15) будем вести методы от противного. Допустим, что существуют такие значения и , что 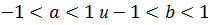, при которых выполняется неравенство

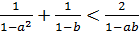. (7.16)

Из неравенства (7.16) получаем

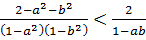. (7.17)

Так как 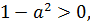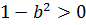и 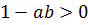, то из неравенство (7.17) следует

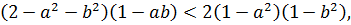
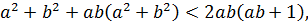
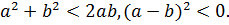
Таким образом, получено ложное неравенство, которое доказывает справедливость исходного неравенства (7.15).